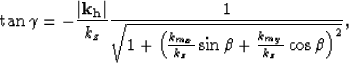Next: artifacts caused by sparsely
Up: Tang: Imaging in the
Previous: introduction
ADCIGs can be extracted either before applying an imaging condition Mosher and Foster (2000); Prucha and Symes (1999); Soubaras (2003); Xie and Wu (2002)
or afterward Biondi and Symes (2004); Sava and Fomel (2003). The advantage of extracting
the angle gathers after the imaging step is that it is a model-space processing, which offers more versatility and generally more efficiency. The
same transformation can be used for images produced by source-receiver migration Sava and Fomel (2003),
shot-profile migration Rickett and Sava (2002)
and reverse time migration Biondi and Shan (2002).
There are basically two steps to extract the angle gathers after imaging: First, compute the SODCIGs. Second, transform the SODCIGs
into ADCIGs. For source-receiver migration, the SODCIGs are immediately available after downward continuation of the wavefields; for
shot-profile migration, a multi-offset imaging condition should be applied to get the SODCIGs Rickett and Sava (2002):
| 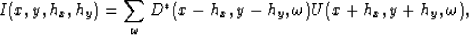 |
(1) |
where I is the image in the subsurface-offset domain, D is the source wavefield, * means the complex conjugate,
U is the receiver wavefield, x, y are the components of midpoint,
hx, hy are the components of subsurface half offset, and 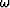 is frequency.
Sava and Fomel (2003) derived the following radial-trace transformation in the Fourier domain to transform the SODCIGs into ADCIGs in 2-D:
is frequency.
Sava and Fomel (2003) derived the following radial-trace transformation in the Fourier domain to transform the SODCIGs into ADCIGs in 2-D:
| 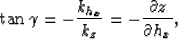 |
(2) |
where 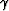 is the reflection angle, khx is the offset wavenumber, and kz is the depth wavenumber.
The transformation is independent of geological dip in 2-D, but the 3-D formulation must be corrected for a crossline dip component.
Tisserant and Biondi (2003) show that we can make this 3-D correction by re-writing the angle-gather transformation as
is the reflection angle, khx is the offset wavenumber, and kz is the depth wavenumber.
The transformation is independent of geological dip in 2-D, but the 3-D formulation must be corrected for a crossline dip component.
Tisserant and Biondi (2003) show that we can make this 3-D correction by re-writing the angle-gather transformation as
| 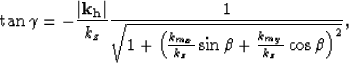 |
(3) |
where 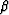 is the reflection azimuth,
is the reflection azimuth, 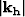 is the absolute value of the offset wavenumber, kmx and kmy
are the components of the midpoint wavenumber.
is the absolute value of the offset wavenumber, kmx and kmy
are the components of the midpoint wavenumber.





Next: artifacts caused by sparsely
Up: Tang: Imaging in the
Previous: introduction
Stanford Exploration Project
5/6/2007