




Next: 2D synthetic tests
Up: Shragge and Shan: Prestack
Previous: Why Elliptic Coordinates?
Propagating wavefields on elliptic meshes using RWE requires
incorporating the geometry of the coordinate system directly in the
extrapolation equations. This section derives the equations for
propagation in the elliptic direction using the non-orthogonal RWE
theory developed in Shragge (2006).
The analytic transformation between elliptic and Cartesian
coordinate systems (see example in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
specified by,
) is
specified by,
| ![\begin{displaymath}
\left[\begin{array}
{c}
x_1\\ x_3
\end{array}\right]
=...
...\,\rm{sinh} \, \xi_3 \, \rm{sin}\,\xi_1 \\ \end{array}\right],\end{displaymath}](img12.gif) |
(3) |
where [x1,x3] are the underlying Cartesian coordinate variables,
![$[\xi_1,\xi_3]$](img13.gif) are the RWE elliptic coordinates, and a is a
stretch parameter controlling the breadth of the coordinate system.
are the RWE elliptic coordinates, and a is a
stretch parameter controlling the breadth of the coordinate system.
The metric tensor (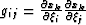 with an implicit sum
over index k) describing the geometry of the elliptic coordinate
system is given by,
with an implicit sum
over index k) describing the geometry of the elliptic coordinate
system is given by,
| ![\begin{displaymath}
\left[g_{ij}\right] =
\left[\begin{array}
{cc}
A^2 & 0\\ 0 & A^2 \\ \end{array}\right],\end{displaymath}](img15.gif) |
(4) |
where 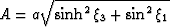 . The
determinant of the metric tensor is
. The
determinant of the metric tensor is 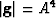 , leading to an
associated (inverse) metric tensor given by,
, leading to an
associated (inverse) metric tensor given by,
| ![\begin{displaymath}
\left[g^{ij}\right] =
\left[\begin{array}
{cc}
A^{-2} & 0 \\ 0 & A^{-2} \\ \end{array}\right].\end{displaymath}](img18.gif) |
(5) |
The weighted metric tensor (the product of the metric tensor and the
determinant: 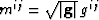 ) is given by,
) is given by,
| ![\begin{displaymath}
\left[m^{ij}\right]
=
\left[\begin{array}
{ccc}
1 & 0 \\ 0 & 1 \\ \end{array}\right].\end{displaymath}](img20.gif) |
(6) |
The corresponding extrapolation wavenumber is generated by using
tensors gij and mij in the wavenumber expression
for general 3D non-orthogonal coordinate systems (equations 13 and 14
in Shragge (2006)). Note that even though the elliptic
coordinate system varies spatially, the local curvature parameters in
the weighted metric tensor are constant. Thus, the extrapolation wavenumber,
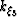 , for recursive wavefield extrapolation stepping outward in
concentric ellipses is,
, for recursive wavefield extrapolation stepping outward in
concentric ellipses is,
| 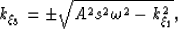 |
(7) |
where 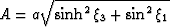 , s
is slowness (inverse of velocity), and
, s
is slowness (inverse of velocity), and 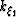 is the
orthogonal wavenumber. Equation 7 is an exact
representation of the extrapolation wavenumber and does not contain
any kinematic approximations. The most striking observation about
this expression is that the sole difference between propagation in
elliptic and Cartesian coordinate systems is a smooth multiplicative
slowness model stretch. Otherwise, existing Cartesian extrapolators
can be used for propagating wavefields.
is the
orthogonal wavenumber. Equation 7 is an exact
representation of the extrapolation wavenumber and does not contain
any kinematic approximations. The most striking observation about
this expression is that the sole difference between propagation in
elliptic and Cartesian coordinate systems is a smooth multiplicative
slowness model stretch. Otherwise, existing Cartesian extrapolators
can be used for propagating wavefields.





Next: 2D synthetic tests
Up: Shragge and Shan: Prestack
Previous: Why Elliptic Coordinates?
Stanford Exploration Project
5/6/2007
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
specified by,
) is
specified by,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
specified by,
) is
specified by,
![]() with an implicit sum
over index k) describing the geometry of the elliptic coordinate
system is given by,
with an implicit sum
over index k) describing the geometry of the elliptic coordinate
system is given by,