




Next: Synthetic Example
Up: Witten: Optimization
Previous: Introduction
The general form of the problem examined by Kim et al. (submitted) is
| 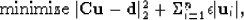 |
(1) |
where 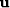 is the model,
is the model, 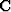 is an operator relating the
model to the data
is an operator relating the
model to the data 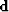 and
and 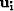 is the model
value at point
is the model
value at point 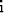 .
.
In this paper a very similar problem, of the form,
| 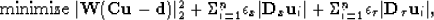 |
(2) |
will be explored. Here 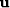 is a vector whose components range over vertical
travel time depth
is a vector whose components range over vertical
travel time depth  and whose values are the interval velocity
squared v2int and
and whose values are the interval velocity
squared v2int and 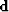 is the data vector which has the same
range as
is the data vector which has the same
range as 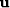 , but whose values are the scaled root-mean squared (RMS) velocities squared,
, but whose values are the scaled root-mean squared (RMS) velocities squared,
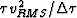 , where
, where 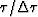 is the index on
the time axis.
is the index on
the time axis. 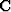 is the casual integration operator, and
is the casual integration operator, and 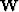 is a weight matrix which is proportional to
our confidence in the RMS velocities. As well,
is a weight matrix which is proportional to
our confidence in the RMS velocities. As well, 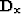 and
and 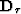 are the first order
finite-difference derivatives along the midpoint and travel-time axis,
respectively, and
are the first order
finite-difference derivatives along the midpoint and travel-time axis,
respectively, and 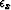 and
and 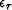 are
the regularization parameters that control the importance of the two
model residuals, effectively controlling the smoothing.
are
the regularization parameters that control the importance of the two
model residuals, effectively controlling the smoothing.
This problem can be transformed to a convex quadratic problem with
linear inequality constraints,
| 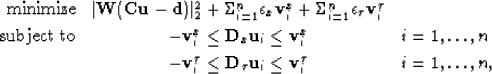 |
|
| |
| (3) |
where 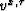 serve to remove the absolute value from the
problem. The new problem (3) can be solved by interior
point methods (e.g. Wright (1997); Ye (1997)). With this goal in mind, we can
now construct
logarithmic barrier functions, which approximate an inequality
constraint by increasing to infinity as the point approaches the
constraint. For a simple problem,
serve to remove the absolute value from the
problem. The new problem (3) can be solved by interior
point methods (e.g. Wright (1997); Ye (1997)). With this goal in mind, we can
now construct
logarithmic barrier functions, which approximate an inequality
constraint by increasing to infinity as the point approaches the
constraint. For a simple problem,
| 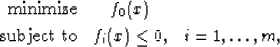 |
|
| (4) |
the logarithmic barrier function is
| 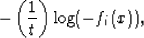 |
(5) |
where t > 0 is a parameter the determines how closely you
approximate the constraint Boyd and Vandenberghe (2004).
For
the bound constraints in equation 3 the barrier functions are:
| 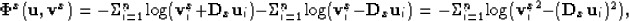 |
(6) |
and
| 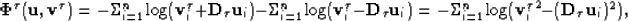 |
(7) |
Now we can define the centering problem as,
| 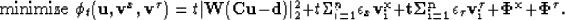 |
(8) |
The centering problem is an equivalent representation to problem
(3) and has a unique
solution parametrized by t, called the central path which leads to
an optimal solution Boyd and Vandenberghe (2004). Newtons method can now be applied
to the centering problem, which involves solving a system on linear
equations,
| ![\begin{displaymath}
H\left[
\begin{array}
{ c }
\Delta \bf{u} \\
\Delta \bf{v}^x \\
\Delta \bf{v}^\tau
\end{array} \right]= -g,
\end{displaymath}](img24.gif) |
(9) |
where 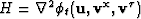 is the Hessian and
is the Hessian and 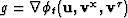 is the gradient. Conjugate gradients is used to find an approximate
solution to this system. We differ from Kim et al. (submitted) by choosing
not to solve the whole system with conjugate gradients. Instead,
is the gradient. Conjugate gradients is used to find an approximate
solution to this system. We differ from Kim et al. (submitted) by choosing
not to solve the whole system with conjugate gradients. Instead, 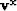 and
and 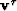 will be
solved analytically, decreasing the size of the system of equations
needed to be solved
solve from 3n to n, substantially reducing computational time.
will be
solved analytically, decreasing the size of the system of equations
needed to be solved
solve from 3n to n, substantially reducing computational time.
`To solve for 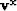 analytically, take the derivative of
analytically, take the derivative of 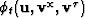 with respect to
with respect to 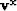 , then solve for
, then solve for 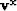 . This gives
. This gives
|  |
(10) |
The same can be done for 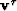 . We can also write the Hessian and gradient succinctly as,
. We can also write the Hessian and gradient succinctly as,
| 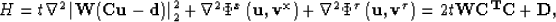 |
(11) |
where
| 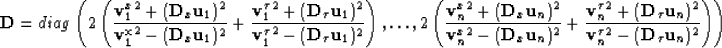 |
(12) |
where diag denotes a diagonal matrix with elements
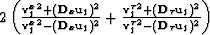 .
The gradient can be written as
.
The gradient can be written as
| ![\begin{eqnarray}
g = &\nabla_u\phi_t({\bf u},{\bf v}^x,{\bf v}^\tau) \nonumber \...
...{2\bf{u}_i}{{\bf{v}^\tau_i}^2-{\bf D}_\tau {\bf u}_i^2}\right]^T.
\end{eqnarray}](img34.gif) |
|
| (13) |
Since the Hessian is constructed from more than the linear operator (it
incorporates the barrier functions),
matrix multiplication is used to solve the system of equations in
the Newton system. Thus each step of the conjugate gradient is slow,
but time is saved by reducing the overall number of conjugate gradient
steps.
The final algorithm is:
given the update parameters for t, set the initial values
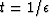 ,
, 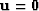 , and
, and 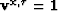 .
.
repeat
1. Calculate 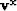 and
and 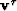
2. Compute the search direction 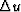 using conjugate gradients
using conjugate gradients
3. Compute the step size s by backtracking line search
4. Update 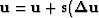 )
)
5. Calculate 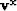 and
and 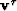 update
update
6. Evaluate the duality gap and quit if appropriate (see Boyd and Vandenberghe (2004)
for more on Duality)
7. Update t





Next: Synthetic Example
Up: Witten: Optimization
Previous: Introduction
Stanford Exploration Project
5/6/2007
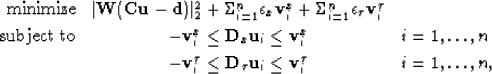
![\begin{displaymath}
H\left[
\begin{array}
{ c }
\Delta \bf{u} \\
\Delta \bf{v}^x \\
\Delta \bf{v}^\tau
\end{array} \right]= -g,
\end{displaymath}](img24.gif)
![]() analytically, take the derivative of
analytically, take the derivative of ![]() with respect to
with respect to ![]() , then solve for
, then solve for ![]() . This gives
. This gives
![\begin{eqnarray}
g = &\nabla_u\phi_t({\bf u},{\bf v}^x,{\bf v}^\tau) \nonumber \...
...{2\bf{u}_i}{{\bf{v}^\tau_i}^2-{\bf D}_\tau {\bf u}_i^2}\right]^T.
\end{eqnarray}](img34.gif)
![]() ,
, ![]() , and
, and ![]() .
.![]() and
and ![]()
![]() using conjugate gradients
using conjugate gradients
![]() )
) ![]() and
and ![]() update
update