The Inverse Problem

The approach to solving the waveform inversion problem followed here Pratt and Worthington (1989) is based on minimizing the residual misfit at each successive frequency, 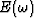$E(\omega)$. Assuming an L₂ norm, the misfit is defined

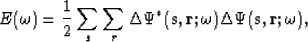$$E(\omega) = \frac{1}{2} \sum_{s} \sum_{r} \Delta \Psi^{*}({\bf s},{\bf r};\omega) \Delta \Psi ({\bf s},{\bf r};\omega) ,$$ (3)

where 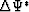$\Delta \Psi^{*}$ denotes complex conjugate of wavefield 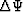$\Delta \Psi$. In this study, I approach the minimization of 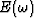$E(\omega)$ through computing the negative gradient, or the direction of greatest decrease of the misfit function, with respect to the variation in model parameters. If model parameters are represented by 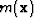$m ({\bf x})$, then the descent direction is defined by

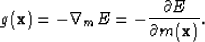$$g ({\bf x}) = -\nabla_m E = - \frac{\partial E}{\partial m ({\bf x})}.$$ (4)

The gradient vector, 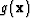$g ({\bf x})$, is considered an image of the model space and can be used to update the model parameter estimates according to  

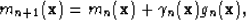$$m_{n+1} ({\bf x}) = m_n ({\bf x}) + \gamma_n ({\bf x}) g_n ({\bf x}),$$ (5)

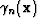where $\gamma_n ({\bf x})$ is the step length discussed below, and subscript n indicates the current iteration number.