




Next: The Inverse Problem
Up: Review of Frequency-domain waveform
Previous: Review of Frequency-domain waveform
The initial step in frequency-domain waveform inversion is to prescribe the forward model. I assume that wave propagation is adequately governed by the acoustic wave equation; thus, any forward-modeling procedure will generate a monochromatic scalar wavefield, 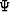 , that is an (approximate) complex-valued solution to the Helmholtz equation,
, that is an (approximate) complex-valued solution to the Helmholtz equation,
| 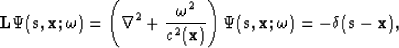 |
(1) |
where 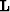 is the Helmholtz operator,
is the Helmholtz operator, 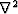 the Laplacian operator,
the Laplacian operator, 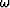 angular frequency,
angular frequency, 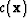 the assumed velocity profile in spatial domain
the assumed velocity profile in spatial domain  ,
,  the source position, and
the source position, and 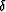 the Dirac delta function operator. Note that the waveform inversion problem is non-linear in model parameters,
the Dirac delta function operator. Note that the waveform inversion problem is non-linear in model parameters, 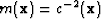 , which I will solve using an iterative inversion approach. Discussion of the specific approach to solving equation 1 being presented is deferred to the following section.
, which I will solve using an iterative inversion approach. Discussion of the specific approach to solving equation 1 being presented is deferred to the following section.
The next step is to compare the modeled wavefield solutions, 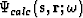 , to the observed data,
, to the observed data, 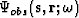 , where
, where  is the receiver position. This procedure leads to a residual wavefield,
is the receiver position. This procedure leads to a residual wavefield, 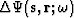 , defined as the difference between the two wavefields
, defined as the difference between the two wavefields
| 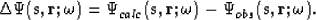 |
(2) |
The residuals are a measure of waveform fit and will be back-projected to generate a velocity model update. Note that no assumption is explicitly made about a linear relation (i.e. the Born approximation is explicitly avoided in the forward modeling problem) Sirgue and Pratt (2004); however, if model parameters are too far removed from the true velocity model, then the monochromatic wavefields in equation 2 will cycle-skip giving erroneous residuals. However, because cycle-skipping is more likely at higher frequencies, the approach is generally more stable at lower frequencies.





Next: The Inverse Problem
Up: Review of Frequency-domain waveform
Previous: Review of Frequency-domain waveform
Stanford Exploration Project
1/16/2007
![]() , to the observed data,
, to the observed data, ![]() , where
, where ![]() is the receiver position. This procedure leads to a residual wavefield,
is the receiver position. This procedure leads to a residual wavefield, ![]() , defined as the difference between the two wavefields
, defined as the difference between the two wavefields