




Next: Examples with real data
Up: Alvarez and Guitton: Adaptive
Previous: Description of the method
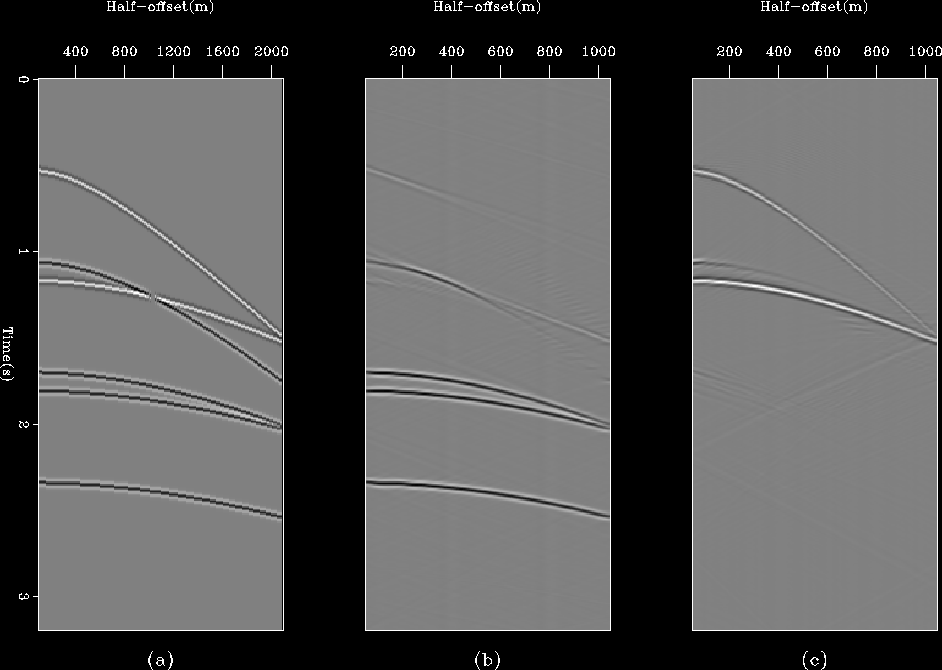
As a first example, we will consider the synthetic dataset shown in
panel (a) of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . There are two primaries (black)
and four multiples (white).
The traveltimes of both primaries and multiples were computed analytically
from a three-layer model: water layer, a sedimentary layer and a half
space.
The estimates of the multiples (b) and primaries (c) were computed by adding
40% of the primaries to the multiples and 40% of the multiples to the
primaries, respectively. The goal is to simulate a situation in which the
kinematics of the
estimates of primaries and multiples are both correct but there is
strong cross-talk (leakage) which may happen, for example, after the multiples
are estimated via filtering in the Radon domain.
syn1_estimates1
. There are two primaries (black)
and four multiples (white).
The traveltimes of both primaries and multiples were computed analytically
from a three-layer model: water layer, a sedimentary layer and a half
space.
The estimates of the multiples (b) and primaries (c) were computed by adding
40% of the primaries to the multiples and 40% of the multiples to the
primaries, respectively. The goal is to simulate a situation in which the
kinematics of the
estimates of primaries and multiples are both correct but there is
strong cross-talk (leakage) which may happen, for example, after the multiples
are estimated via filtering in the Radon domain.
syn1_estimates1
Figure 1 Synthetic CMP gather (a) showing two
primaries (black) and four multiples from a three horizontal layer model.
The initial estimates of multiples (b) and primaries (c) are contaminated
with 40% cross-talk.




 syn1_matched_muls
syn1_matched_muls
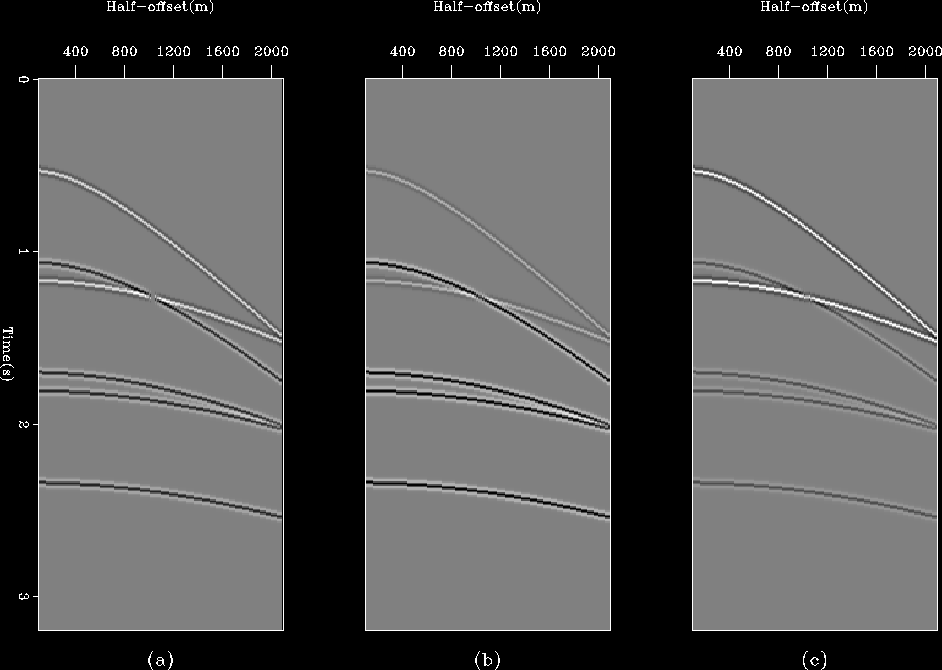
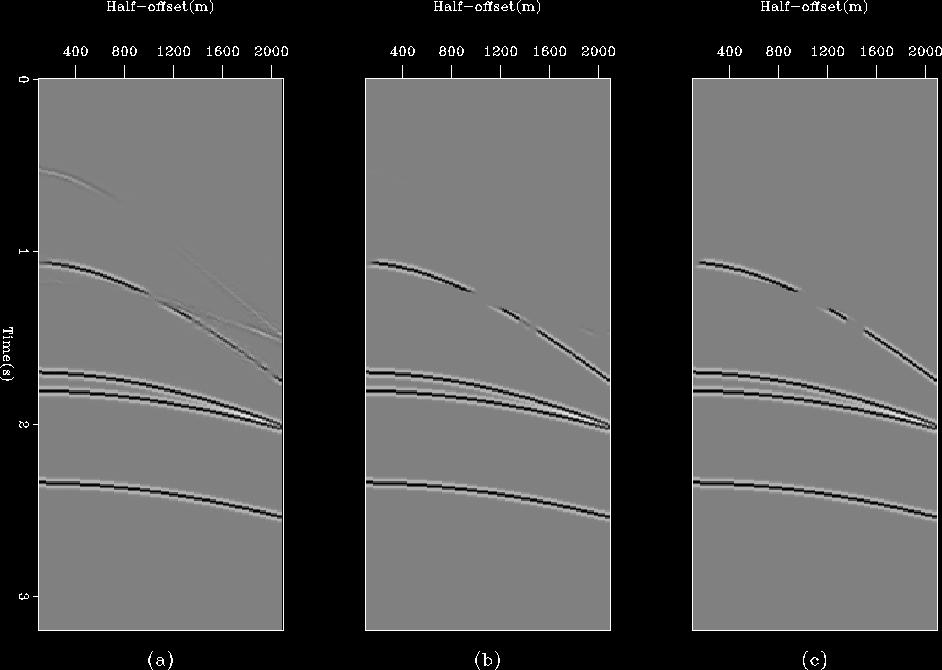
Figure 2 Matched estimates of multiples after
one (a), three (b) and five (c) non-linear iterations of the algorithm.




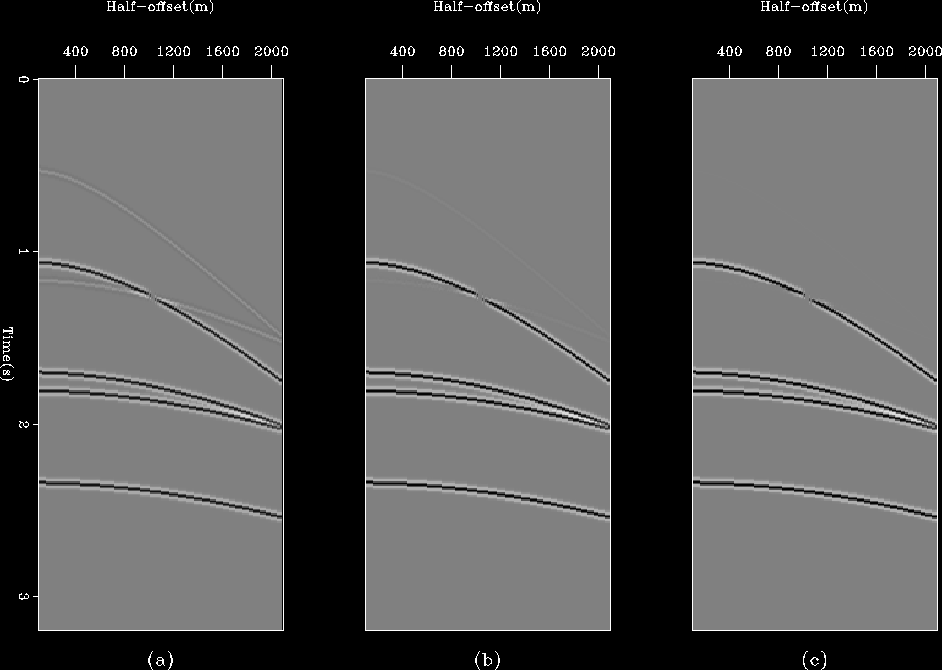
 syn1_matched_prims
syn1_matched_prims
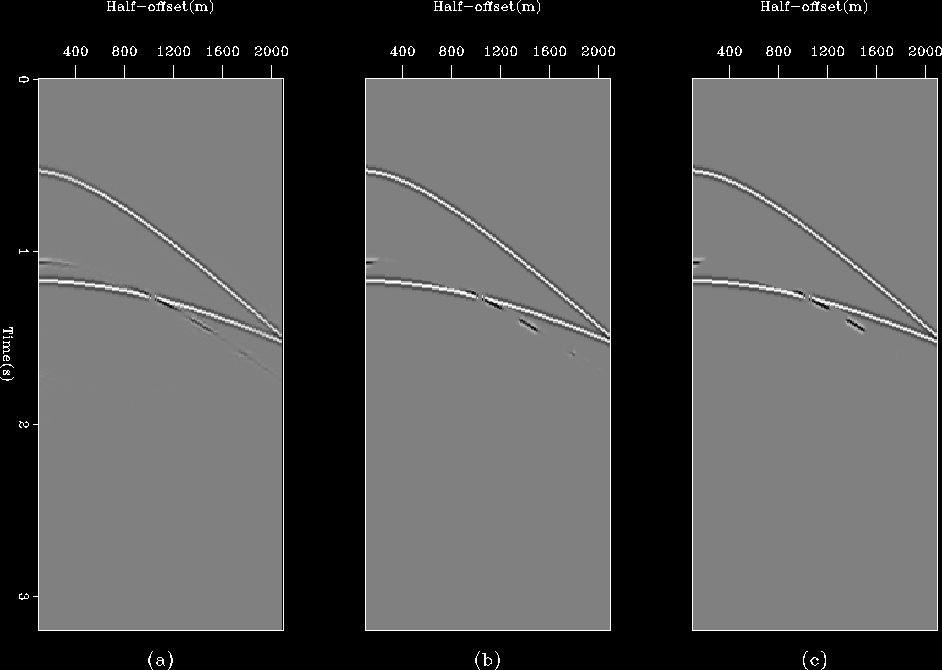
Figure 3 Matched estimates of primaries after
one (a), two (b) and three (c) non-linear iterations of the algorithm.





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the estimated multiples after one,
two and three non-linear iterations of the algorithm. The corresponding
results for the estimated primaries are shown in
Figure
shows the estimated multiples after one,
two and three non-linear iterations of the algorithm. The corresponding
results for the estimated primaries are shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In both figures we see that the
cross-talk is substantially reduced after the first non-linear iteration and
is completely eliminated after the third. Notice the hole in the top multiple
and the bottom primary in the final estimates. This is actually present
in the data (panel (a) in Figure
. In both figures we see that the
cross-talk is substantially reduced after the first non-linear iteration and
is completely eliminated after the third. Notice the hole in the top multiple
and the bottom primary in the final estimates. This is actually present
in the data (panel (a) in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and is an artifact
because both primaries and multiples were modeled with the same amplitude and
opposite polarity.
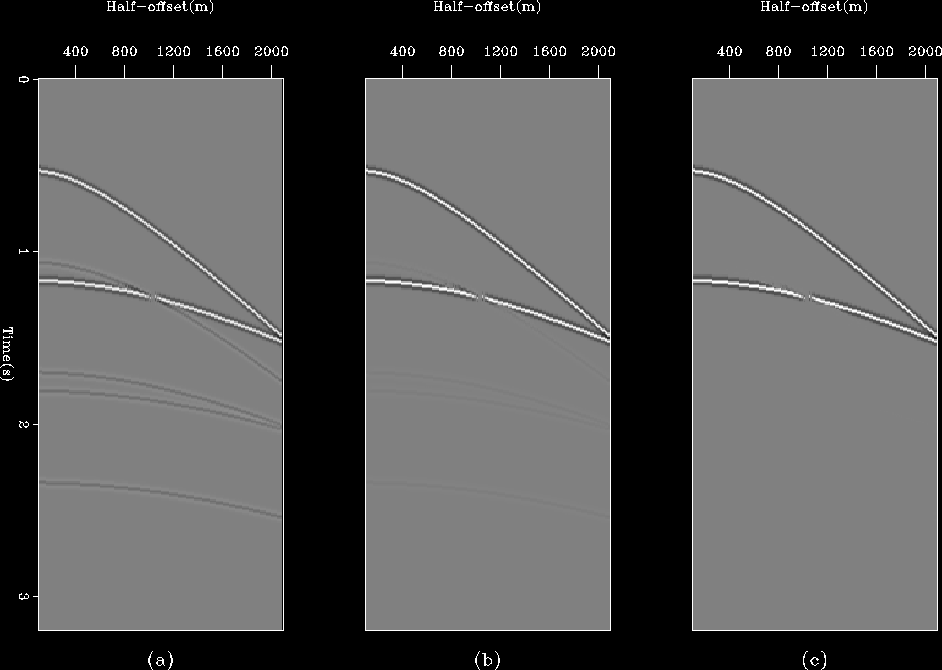
Consider now the more realistic situation of kinematic and offset-dependent
amplitude errors and noise as shown in Figure
) and is an artifact
because both primaries and multiples were modeled with the same amplitude and
opposite polarity.
Consider now the more realistic situation of kinematic and offset-dependent
amplitude errors and noise as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The
multiple and primary estimates were
obtained via migration-demigration as described in a previous report
(). Clearly these are imperfect estimates
with cross-talk on primaries and multiples and other noises.
Panel (a) of Figures
. The
multiple and primary estimates were
obtained via migration-demigration as described in a previous report
(). Clearly these are imperfect estimates
with cross-talk on primaries and multiples and other noises.
Panel (a) of Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the results after one iteration of
the non-linear inversion whereas panels (b) and (c) of the same figures
show the results after three and five non-linear iterations respectively.
There is still some localized cross-talk from the multiples into the
primaries, but given how imperfect the initial estimates were, the result
is encouraging.
show the results after one iteration of
the non-linear inversion whereas panels (b) and (c) of the same figures
show the results after three and five non-linear iterations respectively.
There is still some localized cross-talk from the multiples into the
primaries, but given how imperfect the initial estimates were, the result
is encouraging.
syn2_estimates1
Figure 4 Original CMP gather (a), initial estimate
of multiples (b) and primaries (c).




 syn2_matched_muls
syn2_matched_muls
Figure 5 Matched estimates of multiples after
one (a), three (b) and five (c) non-linear iterations of the algorithm.




 syn2_matched_prims
syn2_matched_prims
Figure 6 Matched estimates of primaries after
one (a), three (b) and five (c) non-linear iterations of the algorithm.





The next example uses the well-known Sigsbee model to illustrate the method
in the image space on an angle stack. The estimate of the multiples was
computed with an image space version of SRME ().
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the modeled data after shot profile
migration (a) and the estimated multiples (b). Both panels are
plotted at the exact same clip value. Notice that the estimate of the multiples
is accurate only in kinematics, not in amplitudes or frequency content.
shows the modeled data after shot profile
migration (a) and the estimated multiples (b). Both panels are
plotted at the exact same clip value. Notice that the estimate of the multiples
is accurate only in kinematics, not in amplitudes or frequency content.
sgsb_estimates1
Figure 7 Migrated angle stack of the Sigsbee model
(a), initial estimates of multiples (b).





sgsb_matched_prims
Figure 8 Estimated primaries after one (a),
two (b) and three (c) iterations of the non-linear inversion.




 sgsb_matched_muls
sgsb_matched_muls
Figure 9 Estimated multiples after one (a),
two (b) and three (c) iterations of the non-linear inversion.





In contrast with the previous examples, in this case we do not have an independent
initial estimate of the primaries. We could subtract the estimates of the multiples
from the data, but the corresponding estimate of the primaries is too distorted
and using it actually hurts the chances of matching the multiples to the data
(since this example is in the image space, ''data'' means the migrated
image with primaries and multiples).
Other option is to use the data itself as the initial estimate of the primaries.
We found, however, that a better alternative is to do a first iteration setting
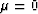 , meaning only the multiples need to be matched. Once matched, the multiples
are subtracted from the data to get the estimate of the primaries for the next
iteration
Figures
, meaning only the multiples need to be matched. Once matched, the multiples
are subtracted from the data to get the estimate of the primaries for the next
iteration
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show a close-up
view of the
matched primaries and multiples, respectively, after one, two and three
non-linear iterations. After the first iteration, the
most obvious multiples contaminating the estimate of the primaries have been
attenuated (compare panels (a) of Figures
show a close-up
view of the
matched primaries and multiples, respectively, after one, two and three
non-linear iterations. After the first iteration, the
most obvious multiples contaminating the estimate of the primaries have been
attenuated (compare panels (a) of Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The second iteration helps attenuate the multiples
further, although is hard to appreciate in these small figures. See, for example the multiple
inside the salt and in the bottom right corner of panel (b). The third iteration does not
help appreciably. The remaining multiples have too much dip and would require a long
filter that could also match the primaries.
On the estimate of the
multiples, again the first iteration extracts the most significant multiples and the second
iteration locally correct the amplitudes. The third iteration actually hurts the estimate
of the multiples because the effect of the regularization term becomes significant as the
match of both the primaries and the multiples to the data improves. The net result is an
estimate of the primaries that is close to the primaries in the original image. The
estimate of the multiples, however, is weaker than it should. If for some reason we wanted the
multiples, we could subtract the estimated primaries from the original image.
). The second iteration helps attenuate the multiples
further, although is hard to appreciate in these small figures. See, for example the multiple
inside the salt and in the bottom right corner of panel (b). The third iteration does not
help appreciably. The remaining multiples have too much dip and would require a long
filter that could also match the primaries.
On the estimate of the
multiples, again the first iteration extracts the most significant multiples and the second
iteration locally correct the amplitudes. The third iteration actually hurts the estimate
of the multiples because the effect of the regularization term becomes significant as the
match of both the primaries and the multiples to the data improves. The net result is an
estimate of the primaries that is close to the primaries in the original image. The
estimate of the multiples, however, is weaker than it should. If for some reason we wanted the
multiples, we could subtract the estimated primaries from the original image.





Next: Examples with real data
Up: Alvarez and Guitton: Adaptive
Previous: Description of the method
Stanford Exploration Project
1/16/2007
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . There are two primaries (black)
and four multiples (white).
The traveltimes of both primaries and multiples were computed analytically
from a three-layer model: water layer, a sedimentary layer and a half
space.
The estimates of the multiples (b) and primaries (c) were computed by adding
40% of the primaries to the multiples and 40% of the multiples to the
primaries, respectively. The goal is to simulate a situation in which the
kinematics of the
estimates of primaries and multiples are both correct but there is
strong cross-talk (leakage) which may happen, for example, after the multiples
are estimated via filtering in the Radon domain.
. There are two primaries (black)
and four multiples (white).
The traveltimes of both primaries and multiples were computed analytically
from a three-layer model: water layer, a sedimentary layer and a half
space.
The estimates of the multiples (b) and primaries (c) were computed by adding
40% of the primaries to the multiples and 40% of the multiples to the
primaries, respectively. The goal is to simulate a situation in which the
kinematics of the
estimates of primaries and multiples are both correct but there is
strong cross-talk (leakage) which may happen, for example, after the multiples
are estimated via filtering in the Radon domain.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the estimated multiples after one,
two and three non-linear iterations of the algorithm. The corresponding
results for the estimated primaries are shown in
Figure
shows the estimated multiples after one,
two and three non-linear iterations of the algorithm. The corresponding
results for the estimated primaries are shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In both figures we see that the
cross-talk is substantially reduced after the first non-linear iteration and
is completely eliminated after the third. Notice the hole in the top multiple
and the bottom primary in the final estimates. This is actually present
in the data (panel (a) in Figure
. In both figures we see that the
cross-talk is substantially reduced after the first non-linear iteration and
is completely eliminated after the third. Notice the hole in the top multiple
and the bottom primary in the final estimates. This is actually present
in the data (panel (a) in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and is an artifact
because both primaries and multiples were modeled with the same amplitude and
opposite polarity.
Consider now the more realistic situation of kinematic and offset-dependent
amplitude errors and noise as shown in Figure
) and is an artifact
because both primaries and multiples were modeled with the same amplitude and
opposite polarity.
Consider now the more realistic situation of kinematic and offset-dependent
amplitude errors and noise as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The
multiple and primary estimates were
obtained via migration-demigration as described in a previous report
(). Clearly these are imperfect estimates
with cross-talk on primaries and multiples and other noises.
Panel (a) of Figures
. The
multiple and primary estimates were
obtained via migration-demigration as described in a previous report
(). Clearly these are imperfect estimates
with cross-talk on primaries and multiples and other noises.
Panel (a) of Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the results after one iteration of
the non-linear inversion whereas panels (b) and (c) of the same figures
show the results after three and five non-linear iterations respectively.
There is still some localized cross-talk from the multiples into the
primaries, but given how imperfect the initial estimates were, the result
is encouraging.
show the results after one iteration of
the non-linear inversion whereas panels (b) and (c) of the same figures
show the results after three and five non-linear iterations respectively.
There is still some localized cross-talk from the multiples into the
primaries, but given how imperfect the initial estimates were, the result
is encouraging.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the modeled data after shot profile
migration (a) and the estimated multiples (b). Both panels are
plotted at the exact same clip value. Notice that the estimate of the multiples
is accurate only in kinematics, not in amplitudes or frequency content.
shows the modeled data after shot profile
migration (a) and the estimated multiples (b). Both panels are
plotted at the exact same clip value. Notice that the estimate of the multiples
is accurate only in kinematics, not in amplitudes or frequency content.



![]() , meaning only the multiples need to be matched. Once matched, the multiples
are subtracted from the data to get the estimate of the primaries for the next
iteration
Figures
, meaning only the multiples need to be matched. Once matched, the multiples
are subtracted from the data to get the estimate of the primaries for the next
iteration
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show a close-up
view of the
matched primaries and multiples, respectively, after one, two and three
non-linear iterations. After the first iteration, the
most obvious multiples contaminating the estimate of the primaries have been
attenuated (compare panels (a) of Figures
show a close-up
view of the
matched primaries and multiples, respectively, after one, two and three
non-linear iterations. After the first iteration, the
most obvious multiples contaminating the estimate of the primaries have been
attenuated (compare panels (a) of Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The second iteration helps attenuate the multiples
further, although is hard to appreciate in these small figures. See, for example the multiple
inside the salt and in the bottom right corner of panel (b). The third iteration does not
help appreciably. The remaining multiples have too much dip and would require a long
filter that could also match the primaries.
On the estimate of the
multiples, again the first iteration extracts the most significant multiples and the second
iteration locally correct the amplitudes. The third iteration actually hurts the estimate
of the multiples because the effect of the regularization term becomes significant as the
match of both the primaries and the multiples to the data improves. The net result is an
estimate of the primaries that is close to the primaries in the original image. The
estimate of the multiples, however, is weaker than it should. If for some reason we wanted the
multiples, we could subtract the estimated primaries from the original image.
). The second iteration helps attenuate the multiples
further, although is hard to appreciate in these small figures. See, for example the multiple
inside the salt and in the bottom right corner of panel (b). The third iteration does not
help appreciably. The remaining multiples have too much dip and would require a long
filter that could also match the primaries.
On the estimate of the
multiples, again the first iteration extracts the most significant multiples and the second
iteration locally correct the amplitudes. The third iteration actually hurts the estimate
of the multiples because the effect of the regularization term becomes significant as the
match of both the primaries and the multiples to the data improves. The net result is an
estimate of the primaries that is close to the primaries in the original image. The
estimate of the multiples, however, is weaker than it should. If for some reason we wanted the
multiples, we could subtract the estimated primaries from the original image.