 |
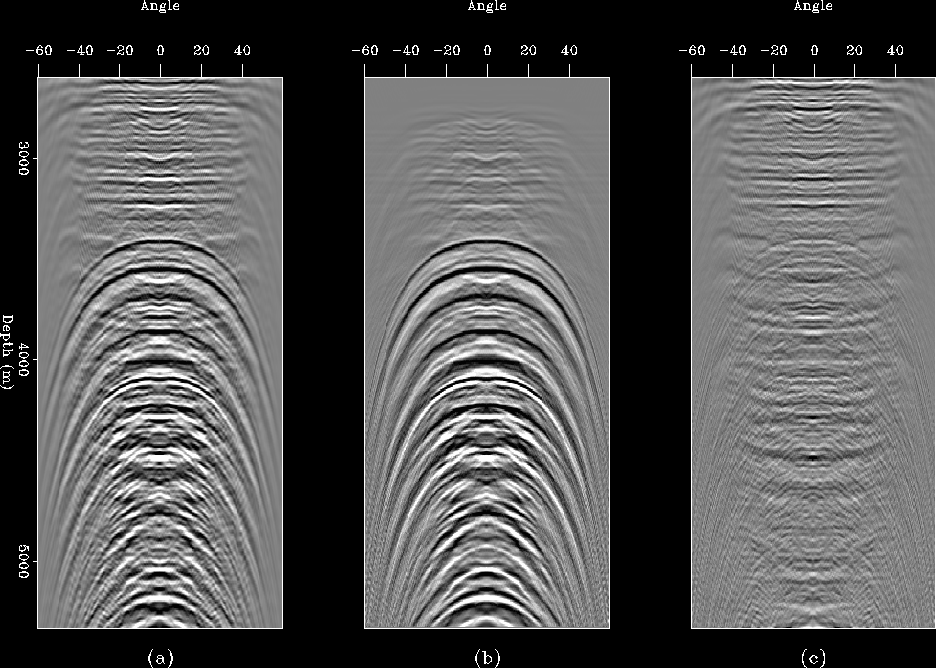
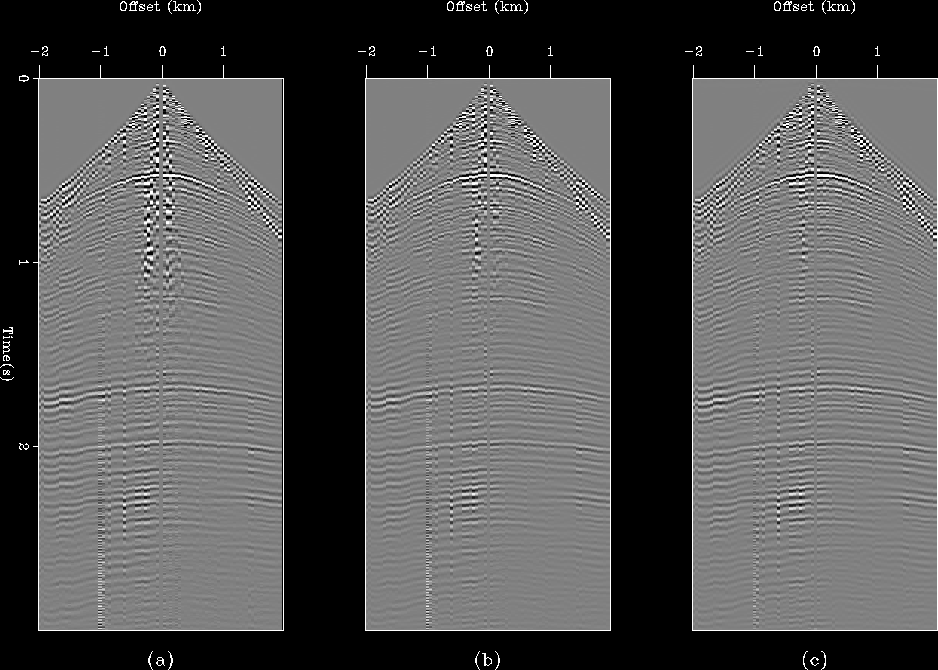
Figure 10 ADCIG (a), initial estimate of the multiples (b), and the primaries (c). Note the crosstalk on both panels.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIG together with the
estimates of the multiples and primaries. The estimate of the multiples
was obtained with an apex-shifted Radon transform in the image space
Alvarez et al. (2004) and the estimate of the primaries was obtained simply
by subtracting it from the data. Notice the residual primary energy just below
3000 m in the estimate of the primaries. Note also the residual energy from the multiples
in the estimate of the primaries.
shows the ADCIG together with the
estimates of the multiples and primaries. The estimate of the multiples
was obtained with an apex-shifted Radon transform in the image space
Alvarez et al. (2004) and the estimate of the primaries was obtained simply
by subtracting it from the data. Notice the residual primary energy just below
3000 m in the estimate of the primaries. Note also the residual energy from the multiples
in the estimate of the primaries.
 |
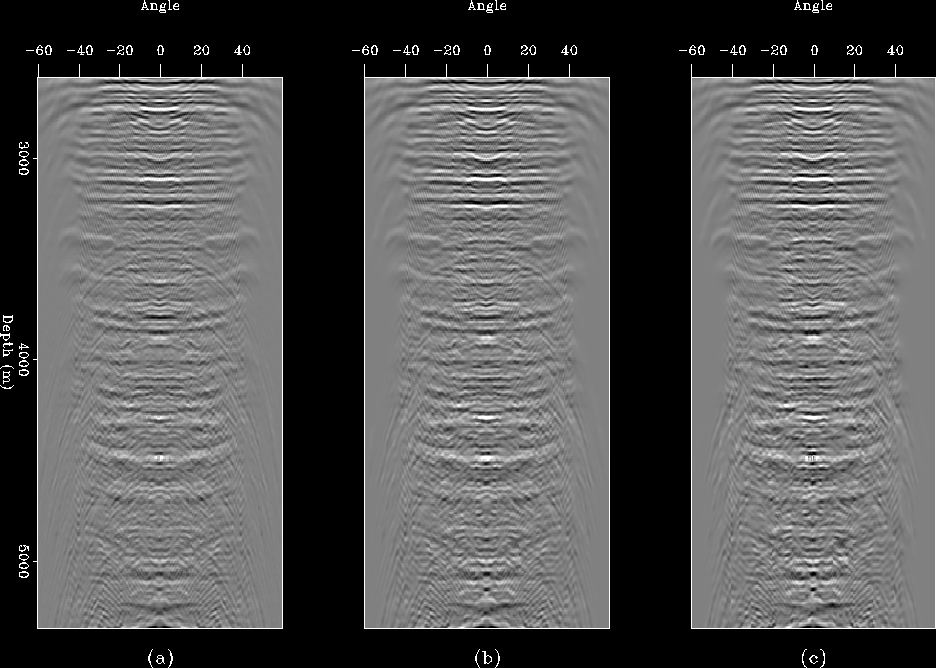 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ADCIG after one, five and ten
non-linear iterations. The first iteration attenuates the
strongest residual multiples (compare panel (a) of
Figure
shows the ADCIG after one, five and ten
non-linear iterations. The first iteration attenuates the
strongest residual multiples (compare panel (a) of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with panel (c) of Figure
with panel (c) of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
 |
Subsequent iterations further reduce the residual
multiples. Also, although hard to see in the hard copy, the primary energy
that contaminated the estimate of multiples below 3000 m has been mapped back to
the primaries.
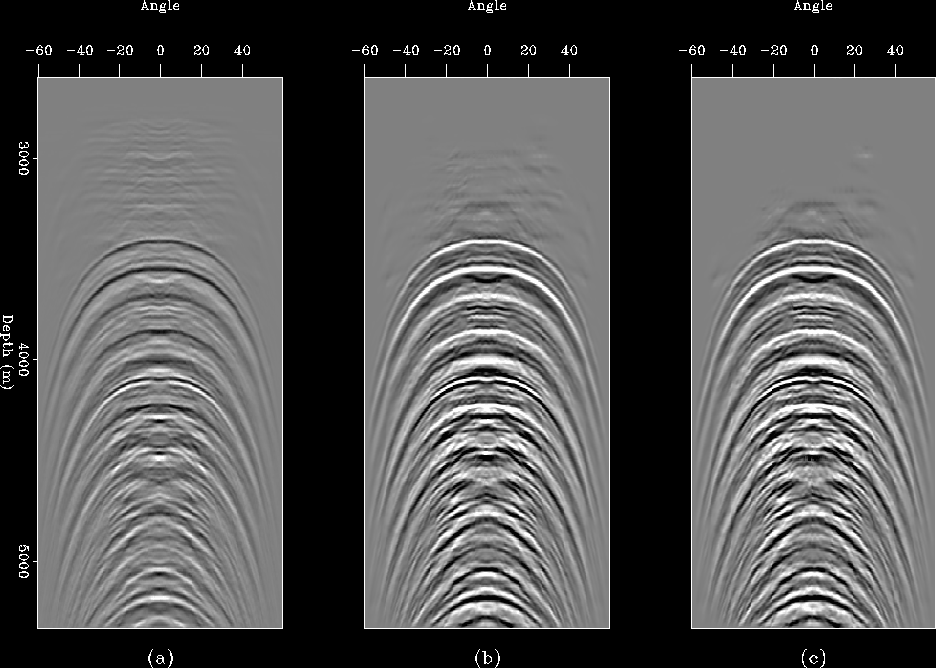
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the corresponding results for the
multiples. Notice again that the residual primary energy has been severely attenuated.
shows the corresponding results for the
multiples. Notice again that the residual primary energy has been severely attenuated.
As a final example, consider the problem of separating ground-roll
from body waves in land data. This a more challenging application of our implementation
of the algorithm because the signal has curvature that changes
rapidly with both offset and time so to match it we need small filters in
relatively small
patches. The ground-roll, on the other hand, has little global curvature
(although it may have strong local curvature due to aliasing) and matching it
is more successful with large filters in large patches.
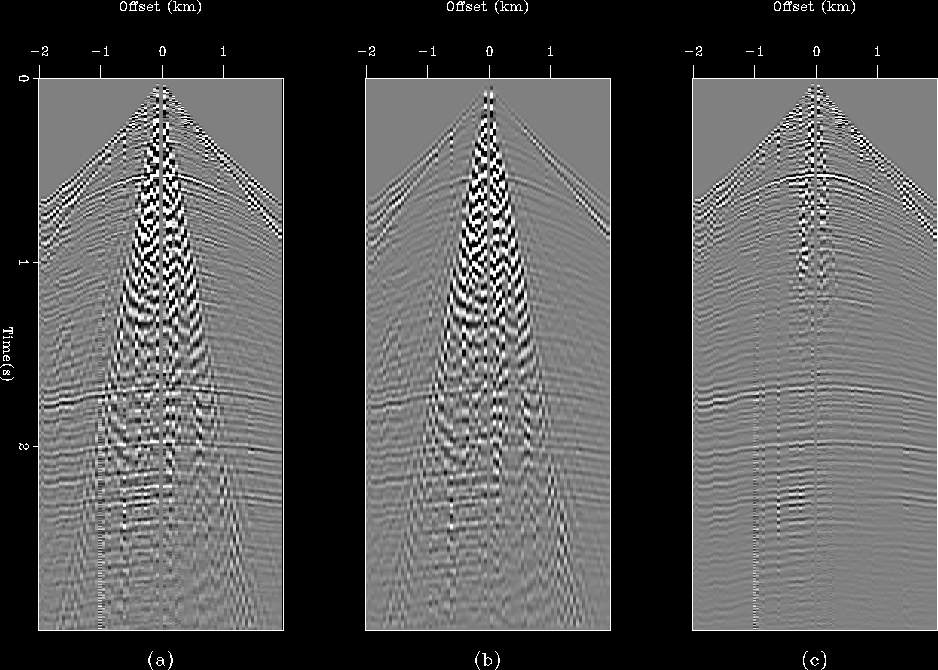
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the original shot as well as the
initial estimates of the body waves and the ground-roll.
shows the original shot as well as the
initial estimates of the body waves and the ground-roll.
 |
 |
The ground-roll estimate was computed simply by high-cut filtering the data to 24 Hz using a Butterworth filter with six poles. We allowed significant energy from the body waves to leak into the estimate of the ground-roll to illustrate the problem described in the previous paragraph. Similarly, the estimate of the body waves was computed by low-cut filtering the data to 18 Hz also with a Butterworth filter with 6 poles. Since we don't want to reduce the low frequency components of the signal too much, we allowed strong ground-roll to leak into the estimate of the body waves. The purpose is to eliminate this ground-roll without hurting the signal and ideally, mapping back some of the body-waves from the estimate of the ground-roll.
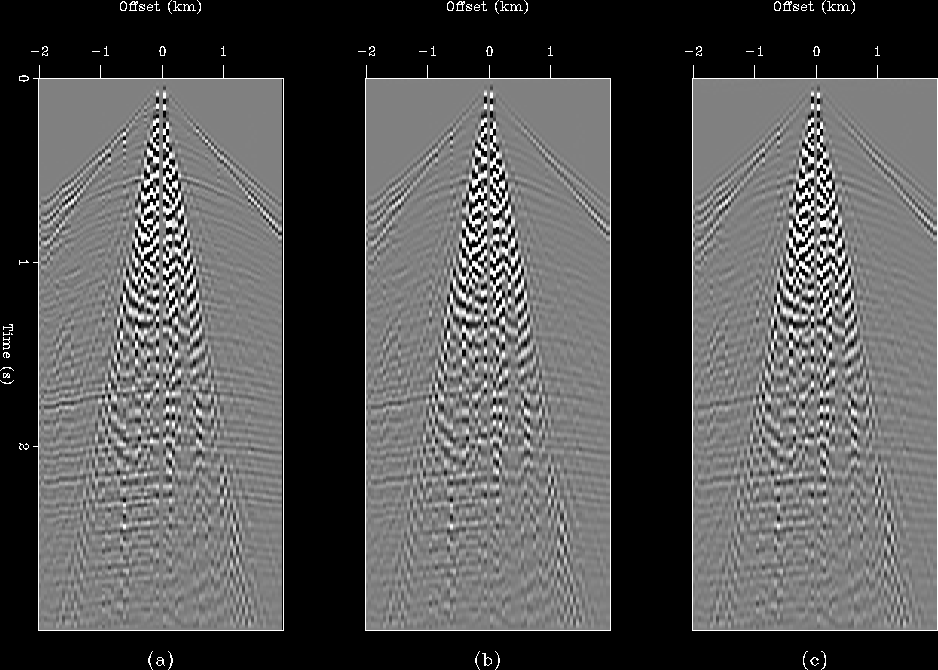 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the estimate of the body-waves
after one, five and 20 non-linear iterations of the proposed algorithm. Even after
just the first iteration, most of the ground-roll has been eliminated and
after five iterations it is almost gone. For this example we used just two
patches in time and one in offset. Figure
shows the estimate of the body-waves
after one, five and 20 non-linear iterations of the proposed algorithm. Even after
just the first iteration, most of the ground-roll has been eliminated and
after five iterations it is almost gone. For this example we used just two
patches in time and one in offset. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
similar results for
the ground-roll. Since the patches were so large, the energy of the leaked
body-waves were only slightly attenuated (see the reflector at about 1.7 secs).
This energy was mapped back to the estimate of the body-waves.
shows
similar results for
the ground-roll. Since the patches were so large, the energy of the leaked
body-waves were only slightly attenuated (see the reflector at about 1.7 secs).
This energy was mapped back to the estimate of the body-waves.