




Next: Examples with synthetic data
Up: Alvarez and Guitton: Adaptive
Previous: Introduction
Conceptually, the first step of our method is to form the convolutional
matrices of both the estimated multiples 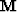 and the estimated primaries
and the estimated primaries
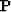 . In practice, these matrices are not explicitly formed but computed with
linear operators Claerbout and Fomel (2002). Next, we compute non-stationary filters in
micro-patches (that is, filters that act locally on overlapping two-dimensional
partitions of the data) to match the estimated multiples and the estimated
primaries, to the data containing both. We compute the filters by solving the
following least-squares inverse problem:
where
. In practice, these matrices are not explicitly formed but computed with
linear operators Claerbout and Fomel (2002). Next, we compute non-stationary filters in
micro-patches (that is, filters that act locally on overlapping two-dimensional
partitions of the data) to match the estimated multiples and the estimated
primaries, to the data containing both. We compute the filters by solving the
following least-squares inverse problem:
where 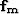 and
and 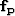 are the matching filters for the
multiples and
primaries respectively,
are the matching filters for the
multiples and
primaries respectively, 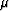 is a parameter to balance the relative
importance of the two components of the fitting goal Guitton (2005),
is a parameter to balance the relative
importance of the two components of the fitting goal Guitton (2005),
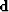 is
the data (primaries and multiples),
is
the data (primaries and multiples), 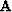 is a regularization
operator, (in our implementation a Laplacian operator), and
is a regularization
operator, (in our implementation a Laplacian operator), and  is the
usual way to control how strong a regularization we want.
is the
usual way to control how strong a regularization we want.
Once convergence is achieved, each filter is applied to its corresponding
convolutional matrix, and new estimates for M and P are computed:
| 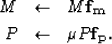 |
(5) |
| (6) |
These updated versions of M and P are then plugged into
equations 1 and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and the process repeated until the
cross-talk has been eliminated or significantly attenuated.
and the process repeated until the
cross-talk has been eliminated or significantly attenuated.





Next: Examples with synthetic data
Up: Alvarez and Guitton: Adaptive
Previous: Introduction
Stanford Exploration Project
1/16/2007
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and the process repeated until the
cross-talk has been eliminated or significantly attenuated.
and the process repeated until the
cross-talk has been eliminated or significantly attenuated.