To predict multiples in the image space, the transform from the
data space (shot gathers) to the image space plays an
integral role. The image space is the output of migration, which in
this implementation, is produced with a shot-profile depth migration
algorithm. Shot-profile wave-equation depth migration
Claerbout (1971) is the cascade of two component operations:
extrapolation, and imaging. The extrapolation is carried out with an
anticausal wave-equation operator on the up-going wavefield, U, and
a causal operator for the down-going wavefield, D. U is a shot
record with traces placed along a wavefield axis ![]() . D is
a zero valued wavefield, also defined along the axis
. D is
a zero valued wavefield, also defined along the axis ![]() where
a source function is placed at the location of the shot being
migrated,
where
a source function is placed at the location of the shot being
migrated, ![]() . The wavefields are recursively extrapolated to
all depths z using the one-way Fourier domain solution to the
wave-equation
. The wavefields are recursively extrapolated to
all depths z using the one-way Fourier domain solution to the
wave-equation
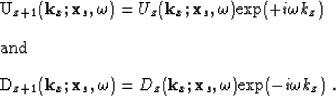 |
(1) | |
| (2) |
The correlation based multi-offset imaging condition for shot-profile migration at each depth level z is Rickett and Sava (2002)
| |
(3) |
SRME is also a two component process: Multiple prediction and subtraction. Acknowledging the approximation of autoconvolving raw data traces rather than convolving data with only primaries, the prediction step (SRMP) can be written in the Fourier domain (Berkhout and Verschuur, equation 13f, 1997)
| |
(4) |
Wave-equation extrapolation is performed on wavefields where data and
source-functions are used as initial conditions to propagate energy
into the subsurface. To begin, traces at locations ![]() are
inserted into a zero-valued wavefield defined along the axis
are
inserted into a zero-valued wavefield defined along the axis ![]() as depicted in Figure 1. Although data-space SRMP is a
trace-by-trace operation, equation 4 can be redefined in
terms of the wavefield
as depicted in Figure 1. Although data-space SRMP is a
trace-by-trace operation, equation 4 can be redefined in
terms of the wavefield ![]() . Because null-traces
occupy locations
. Because null-traces
occupy locations ![]() at which no data were collected, a multiple
prediction can be also be written
at which no data were collected, a multiple
prediction can be also be written
| |
(5) |
|
GEO-2006-0199-fig1
Figure 1 Traces from a shot-gather at locations | 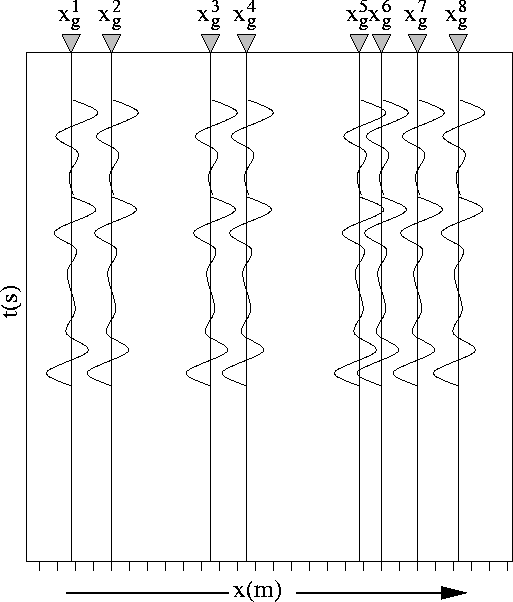 |
Using the principle of reciprocity between the receiver and source locations (first and second arguments of the wavefields respectively), the multiple prediction becomes
| |
(6) |
| |
(7) |
| |
(8) |
Extrapolation by the exponential phase-shift operator
![]() , in equation 1, simply redatums the
shot-gather U. Image-space SRMP (IS-SRMP) is the application of a
second imaging condition evaluated at each subsurface depth level
during the migration that images only multiples. It is the chain of
multiple prediction (convolution) and zero-time extraction (summation
over frequency). The image-space multiple prediction, as a function of
sub-surface offset, is therefore
, in equation 1, simply redatums the
shot-gather U. Image-space SRMP (IS-SRMP) is the application of a
second imaging condition evaluated at each subsurface depth level
during the migration that images only multiples. It is the chain of
multiple prediction (convolution) and zero-time extraction (summation
over frequency). The image-space multiple prediction, as a function of
sub-surface offset, is therefore
| |
(9) |
There are two important ramifications for the equation for predicting multiples with the imaging condition above. The first, is that this operation is intrinsically a shot-domain manipulation of the data. After sorting to CMP-offset coordinates, the source and receiver coordinates are mixed in such a way as to make IS-SRMP invalid for survey-sinking style migration algorithms. Second, because reciprocity was invoked to derive equation 9, off-end (marine) acquisition geometries will need to have split-spread gathers manufactured via reciprocity. The split-spread gathers will include the ray-paths from multiples that emerge in front of the receiver spread (boat) which need to be included in the shot-gathers to predict all possible multiple events.
Further understanding of the IS-SRMP imaging condition for those
familiar with shot-profile migration algorithms can be elicited by
defining the down-going wavefield in equations 1 & 2 by
![]() . Therefore, equations 1 - 3
become
. Therefore, equations 1 - 3
become
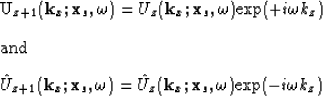 |
(10) | |
| (11) |
| |
(12) |
Because the conjugation of D in the imaging condition of equation 3 can be commuted with the causality of the extrapolation operator, it is not practically necessary to extrapolate U in two different directions. Instead, the second extrapolation step can be ignored
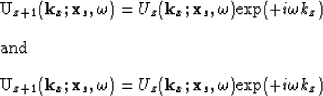 |
(13) | |
| (14) |
| |
(15) |
The migration defined by the chain of these extrapolation and imaging
steps is exactly that for conventional migration where ![]() ,
instead of a modeled source function. Cast in this manner, the
migration shows similarity with reverse-time migration
Baysal et al. (1983) and using multiples to migrate primaries
Shan and Guitton (2004). The difference is in not time-reversing the
data to use as the source function. IS-SRMP uses primaries as areal
source functions and data to image multiples when energy is colocated
in the wavefields after extrapolation.
,
instead of a modeled source function. Cast in this manner, the
migration shows similarity with reverse-time migration
Baysal et al. (1983) and using multiples to migrate primaries
Shan and Guitton (2004). The difference is in not time-reversing the
data to use as the source function. IS-SRMP uses primaries as areal
source functions and data to image multiples when energy is colocated
in the wavefields after extrapolation.