




Next: Analytic example
Up: Image-space SRMP
Previous: Image-space SRMP
One of the reasons that multiple predictions must be adaptively
subtracted from the data is that the wavelet in the data is
squared during the convolution. To address the problem, we introduce
deconvolution to both the conventional Guitton et al. (2006); Lee et al. (1991)
and the multiple prediction imaging conditions.
To normalize the frequency content and provide a sharper image, the
imaging condition in equation 3 becomes
| 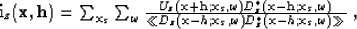 |
(16) |
where the denominator is smoothed across horizontal coordinates for
stability. In this implementation, the smoothing operator is a
triangle function with a base five samples wide. Equation 9
can similarly be normalized/deconvolved and implemented
| 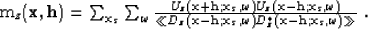 |
(17) |
It could be argued that the deconvolutional imaging condition for
multiples above should be normalized by a smoothed version of the
power spectrum of U instead of D. However, in the interest of parallel
construction, we have implemented it as above. If the wavelet used to
model D accurately represents the amplitude and frequency content of
the data, the choice of U or D as divisor will be of little
importance. The benefit of a deconvolution imaging condition is to
collapse the wavelet that events are convolved with as much as
possible. Consequently, the image-space volumes 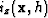 and
and
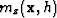 share approximately the same bandwidth and can be
more easily subtracted from each other to provide an image space
consisting of only primaries. If the data are not zero-phase before
implementing IS-SRMP, deconvolution will not address phase-roll of the
wavelet within the data introduced by squaring to compute the multiple
prediction.
share approximately the same bandwidth and can be
more easily subtracted from each other to provide an image space
consisting of only primaries. If the data are not zero-phase before
implementing IS-SRMP, deconvolution will not address phase-roll of the
wavelet within the data introduced by squaring to compute the multiple
prediction.





Next: Analytic example
Up: Image-space SRMP
Previous: Image-space SRMP
Stanford Exploration Project
1/16/2007