




Next: EXAMPLE: WEBER SANDSTONE
Up: Berryman: Geomechanical analysis with
Previous: DOUBLE-POROSITY GEOMECHANICS
Elasticity of layered materials
Next, to determine the overall drained (or undrained) bulk and
shear moduli of the reservoir,
assume a typical building block of the random system is a
small (relative to the size of the reservoir)
``grain'' of laminate material whose elastic response
for a transversely isotropic (hexagonal) system can be
described locally by:
|  |
(18) |
where 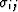 are the usual stress components for
i,j=1-3 in Cartesian coordinates, with 3 (or z) being
the axis of symmetry (the lamination direction for such a
layered material). Displacement ui is then related to strain
component eij by
are the usual stress components for
i,j=1-3 in Cartesian coordinates, with 3 (or z) being
the axis of symmetry (the lamination direction for such a
layered material). Displacement ui is then related to strain
component eij by
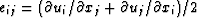 .This definition introduces some convenient factors of two into the
44,55,66 components of the matrix of stiffness coefficients shown in
(18).
For definiteness I also assume that the matrix of stiffness
coefficients in (18) arises from
the lamination of N isotropic constituents having bulk and shear
moduli Kn,
.This definition introduces some convenient factors of two into the
44,55,66 components of the matrix of stiffness coefficients shown in
(18).
For definiteness I also assume that the matrix of stiffness
coefficients in (18) arises from
the lamination of N isotropic constituents having bulk and shear
moduli Kn, 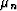 , in the N > 1 layers present in each
building block. It is important that the thicknesses dn always be
in the same proportion in each of these laminated blocks, so that
, in the N > 1 layers present in each
building block. It is important that the thicknesses dn always be
in the same proportion in each of these laminated blocks, so that
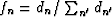 . But the order in which
layers were added to the blocks is not important, as
Backus's formulas (Backus, 1962) for the constants show. For the overall
quasistatic (long wavelength) behavior of the system
I am studying, Backus's results [also see
Postma (1955), Berryman (1998; 2004b), Milton (2002)]
state that
. But the order in which
layers were added to the blocks is not important, as
Backus's formulas (Backus, 1962) for the constants show. For the overall
quasistatic (long wavelength) behavior of the system
I am studying, Backus's results [also see
Postma (1955), Berryman (1998; 2004b), Milton (2002)]
state that
| 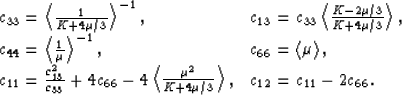 |
(19) |
This bracket notation can be correctly viewed as a line integral along the symmetry axis x3.
The bulk modulus Kn and shear modulus 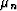 displayed in these
averages can be either the drained or the undrained moduli for the
individual layers. For the undrained case, the results are inherently
assumed either to apply at very high frequencies, such as ultrasonic frequencies
in laboratory experiments, or to situations wherein each layer is
physically isolated so that fluid increments cannot move from one
porous layer to the next.
The bulk modulus for each laminated grain is that given
by the compressional Reuss average KR
of the corresponding compliance matrix sij [the inverse of the
usual stiffness matrix cij, whose nonzero components are
shown in (18)]. The result is
displayed in these
averages can be either the drained or the undrained moduli for the
individual layers. For the undrained case, the results are inherently
assumed either to apply at very high frequencies, such as ultrasonic frequencies
in laboratory experiments, or to situations wherein each layer is
physically isolated so that fluid increments cannot move from one
porous layer to the next.
The bulk modulus for each laminated grain is that given
by the compressional Reuss average KR
of the corresponding compliance matrix sij [the inverse of the
usual stiffness matrix cij, whose nonzero components are
shown in (18)]. The result is
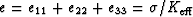 , where
, where
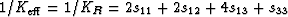 .Even though
.Even though 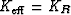 is the same for every grain, since the
grains themselves are not isotropic, the overall bulk modulus
K* of the random polycrystal does not necessarily have the same
value as KR for the individual grains (Hill, 1952). Hashin-Shtrikman bounds on K* for random polycrystals whose
grains have hexagonal symmetry (Peselnick and Meister, 1965; Watt and
Peselnick, 1980)
show in fact that the KR value lies outside the bounds
in many situations (Berryman, 2004).
is the same for every grain, since the
grains themselves are not isotropic, the overall bulk modulus
K* of the random polycrystal does not necessarily have the same
value as KR for the individual grains (Hill, 1952). Hashin-Shtrikman bounds on K* for random polycrystals whose
grains have hexagonal symmetry (Peselnick and Meister, 1965; Watt and
Peselnick, 1980)
show in fact that the KR value lies outside the bounds
in many situations (Berryman, 2004).
Bounds for random polycrystals
Voigt and Reuss bounds: hexagonal symmetry:
For hexagonal symmetry, the nonzero stiffness constants are:
c11, c12, c13 = c23, c33, c44 = c55, and
c66 = (c11-c12)/2.
The Voigt (1928) average for bulk modulus of hexagonal systems is well-known to be
| ![\begin{displaymath}
K_V = \left[2(c_{11}+c_{12}) +4c_{13}+c_{33}\right]/9.
\end{displaymath}](img40.gif) |
(20) |
Similarly, for the overall shear modulus G*, I have
| 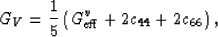 |
(21) |
where the new term appearing here is essentially defined by
(21) and given explicitly by
| 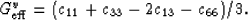 |
(22) |
The quantity 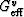 is the energy per unit volume in a grain when
a ``pure uniaxial shear'' strain of unit magnitude [i.e.,
is the energy per unit volume in a grain when
a ``pure uniaxial shear'' strain of unit magnitude [i.e.,
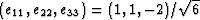 ], whose main compressive
strain is applied to the grain along its axis of symmetry
(Berryman, 2004a; 2004b). Note that the concept of ``pure uniaxial shear'' strain (or stress) is
based on the observation that if a uniaxial principal strain (or stress) of
magnitude 3 is applied along the symmetry axis, it can be decomposed
according to (0,0,3)T = (1,1,1)T - (1,1,-2)T into a pure
compression and a pure shear contribution, which is then called
for the sake of brevity the ``pure uniaxial shear.''
The Reuss (1929) average KR for bulk modulus can also be written
in terms of stiffness coefficients as
], whose main compressive
strain is applied to the grain along its axis of symmetry
(Berryman, 2004a; 2004b). Note that the concept of ``pure uniaxial shear'' strain (or stress) is
based on the observation that if a uniaxial principal strain (or stress) of
magnitude 3 is applied along the symmetry axis, it can be decomposed
according to (0,0,3)T = (1,1,1)T - (1,1,-2)T into a pure
compression and a pure shear contribution, which is then called
for the sake of brevity the ``pure uniaxial shear.''
The Reuss (1929) average KR for bulk modulus can also be written
in terms of stiffness coefficients as
| 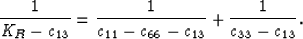 |
(23) |
The Reuss average for shear is
| ![\begin{displaymath}
G_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^r} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img46.gif) |
(24) |
that defines
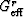 -
i.e., the energy per unit volume in a grain when a pure uniaxial
shear stress of unit magnitude [i.e.,
-
i.e., the energy per unit volume in a grain when a pure uniaxial
shear stress of unit magnitude [i.e.,
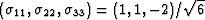 ],
whose main compressive pressure is applied to a grain along
its axis of symmetry.
For each grain having hexagonal symmetry, two product formulas found
by Berryman (2004a) hold:
],
whose main compressive pressure is applied to a grain along
its axis of symmetry.
For each grain having hexagonal symmetry, two product formulas found
by Berryman (2004a) hold:
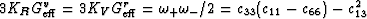 .The symbols
.The symbols 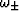 stand for the quasi-compressional and
quasi-uniaxial-shear eigenvalues for the crystalline grains.
Thus, it follows that
stand for the quasi-compressional and
quasi-uniaxial-shear eigenvalues for the crystalline grains.
Thus, it follows that
| 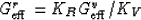 |
(25) |
is a general formula, true for hexagonal symmetry. Hashin-Shtrikman bounds:
It has been shown elsewhere (Berryman, 2004a; 2004b)
that the Peselnick-Meister-Watt (Peselnick and Meister, 1965;
Watt and Peselnick, 1980)
bounds for bulk modulus of a random
polycrystal composed of hexagonal (or transversely isotropic)
grains are given by
| 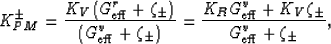 |
(26) |
where 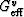 (
(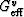 ) is the uniaxial shear energy per
unit volume for a unit applied shear strain (stress).
The second equality follows directly from the product formula
(25). Parameters
) is the uniaxial shear energy per
unit volume for a unit applied shear strain (stress).
The second equality follows directly from the product formula
(25). Parameters 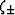 are defined by
are defined by
| 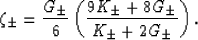 |
(27) |
In (27), values of 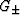 (shear moduli of isotropic
comparison materials) are given by inequalities
(shear moduli of isotropic
comparison materials) are given by inequalities
| 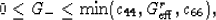 |
(28) |
and
| 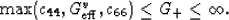 |
(29) |
The values of 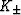 (bulk moduli of isotropic
comparison materials) are then given by algorithmic equalities
(bulk moduli of isotropic
comparison materials) are then given by algorithmic equalities
| 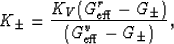 |
(30) |
derived by Peselnick and Meister (1965) and Watt and Peselnick (1980). Also see Berryman (2004a). Bounds 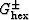 (+ is upper bound, - is the lower bound)
on the shear moduli for random polycrystals
of hexagonal crystals are then given by
(+ is upper bound, - is the lower bound)
on the shear moduli for random polycrystals
of hexagonal crystals are then given by
| ![\begin{displaymath}
\frac{1}{G_{\rm hex}^\pm + \zeta_\pm} =
\frac{1}{5}\Big[\fr...
...\frac{2}{c_{44}+\zeta_\pm} + \frac{2}{c_{66}+\zeta_\pm}\Big],
\end{displaymath}](img61.gif) |
(31) |
where 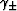 and
and 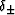 are given by
are given by
| 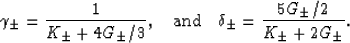 |
(32) |
KV is the Voigt average of the bulk modulus as defined previously.
1.4
T
ABLE 1. Input Parameters for Weber Sandstone Model
of Double-Porosity System.
| Ks |
Ks(1) |
Kd(1) |
Gd(1) |
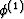 |
Ks(2) |
Kd(2) |
Gd(2) |
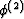 (GPa) (GPa) |
Note: Porosity
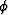
is dimensionless.





Next: EXAMPLE: WEBER SANDSTONE
Up: Berryman: Geomechanical analysis with
Previous: DOUBLE-POROSITY GEOMECHANICS
Stanford Exploration Project
10/31/2005


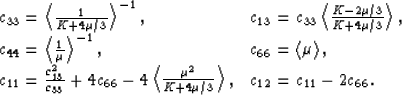
![\begin{displaymath}
G_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^r} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img46.gif)