




Next: [3] The meaning and
Up: Aspects of Linearized migration/inversion
Previous: [1] Numerical calculation of
The linearized migration/inversion can be formulated from the integral expressed in equation (15). It can be regarded as an inverse generalized Radon transform. Equation (15) can be expressed as a matrix equation. The process for solving the equation set is just the migration/inversion imaging.
Following Berkhout (1997), we first give a matrix expression of wave propagation from a source to a scatterer and then to a receiver:
| ![\begin{displaymath}
W^{U}R\left(\theta \right)W^{D} =\left[ \begin{array}
{llcl}...
..._{Q1} & g^{D}_{Q2} & \cdots & g^{D}_{QN} \\ \end{array}\right],\end{displaymath}](img133.gif) |
(58) |
where WU is a discretized Green's function for upward wave propagation, WD is a discretized Green's function for downward wave propagation, and 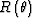 is a reflectivity matrix, which is related to the incident angle. If the variation of reflectivity with angle is neglected,
is a reflectivity matrix, which is related to the incident angle. If the variation of reflectivity with angle is neglected, 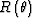 becomes a diagonal matrix. The reflectivity in this case is assumed to be the normal reflectivity. In practice, the reflectivity of a reflector varies with the incident angle. This is called an AVO/AVA phenomenon in seismology. The prestack migration/inversion aims at estimating the angle reflectivity to evaluate lithological variations. On the other hand, the residual moveout of the angle reflectivity indicates whether the macro migration/inversion velocity is reasonable or not.
The synthetic wave field can be written as follows:
becomes a diagonal matrix. The reflectivity in this case is assumed to be the normal reflectivity. In practice, the reflectivity of a reflector varies with the incident angle. This is called an AVO/AVA phenomenon in seismology. The prestack migration/inversion aims at estimating the angle reflectivity to evaluate lithological variations. On the other hand, the residual moveout of the angle reflectivity indicates whether the macro migration/inversion velocity is reasonable or not.
The synthetic wave field can be written as follows:
| ![\begin{displaymath}
P\left(\vec{x}_{r},\vec{x}_{s},\omega \right) =\sum\limits_{...
... \left( g^{U}rg^{D}\right) _{MN} \\ \end{array}\right]_{i_{z}}.\end{displaymath}](img135.gif) |
(59) |
In equation (59), each element of the matrix P is a recorded seismic trace in the time domain and a recorded amplitude value for a shot-receiver pair in the frequency domain. Each column is a shot gather, and each row is a common receiver gather. Therefore, equation (59) can be regarded as the matrix expression of equation (15).
The classical prestack migration can be formulated as the following:
| ![\begin{displaymath}
\left[ W^{U}\left( z_{0},z_{1}\right) \right] ^{H}P\left(\ve...
...}\left( z_{1},z_{0}\right) \right]^{H} = R\left( z_{1} \right).\end{displaymath}](img136.gif) |
(60) |
The detailed matrix expression of equation (60) is
| ![\begin{eqnarray}
&&\left[ \begin{array}
{llcl}
\tilde{g}^{U}_{11} & \tilde{g}^{U...
...otfill \\ r_{P1} & r_{P2} & \cdots & r_{PQ} \\ \end{array}\right],\end{eqnarray}](img137.gif) |
|
| (61) |
where 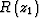 is the image of the first layer. In
is the image of the first layer. In 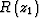 , each row is an angle gather at an imaging point, and each column is a common angle gather. The multiplication of the pth row in the matrix
, each row is an angle gather at an imaging point, and each column is a common angle gather. The multiplication of the pth row in the matrix ![$\left[ W^{U}\left( z_{0},z_{1}\right) \right] ^{H}$](img139.gif) by any column in the matrix
by any column in the matrix 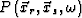 corresponds to a detection focusing of a shot gather; the multiplication of the qth column in the matrix
corresponds to a detection focusing of a shot gather; the multiplication of the qth column in the matrix ![$\left[ W^{D}\left( z_{1},z_{0}\right) \right]^{H}$](img141.gif) by any row in the matrix
by any row in the matrix 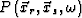 corresponds to an emission focusing.
Then, the image of the second layer can be obtained with
corresponds to an emission focusing.
Then, the image of the second layer can be obtained with
| ![\begin{displaymath}
\left[ W^{U}\left(z_{0},z_{2}\right) \right] ^{H}P\left(\vec...
...D}\left(z_{2},z_{0}\right) \right]^{H} = R\left( z_{2} \right).\end{displaymath}](img142.gif) |
(62) |
Generally, the image of the zith layer is
| ![\begin{displaymath}
\left[ W^{U}\left( z_{0},z_{i}\right) \right]^{H} P\left(\ve...
...}\left( z_{i},z_{0}\right) \right]^{H} = R\left( z_{i} \right).\end{displaymath}](img143.gif) |
(63) |
Here, the matrices ![$\left[ W^{U} \right]^{H}$](img144.gif) and
and ![$\left[ W^{D} \right]^{H}$](img145.gif) are non-recursive. Otherwise, equation (62) and (63) will be of the following forms:
are non-recursive. Otherwise, equation (62) and (63) will be of the following forms:
| ![\begin{displaymath}
\left[ W^{U}\left( z_{1},z_{2}\right) \right] ^{H}\left[ W^{...
...}\left( z_{2},z_{1}\right) \right]^{H} = R\left( z_{2} \right),\end{displaymath}](img146.gif) |
(64) |
or
| ![\begin{displaymath}
\left[ W^{U}\left( z_{1},z_{2}\right) \right] ^{H}P\left(\ve...
...}\left( z_{2},z_{1}\right) \right]^{H} = R\left( z_{2} \right),\end{displaymath}](img147.gif) |
(65) |
and
| ![\begin{displaymath}
\left[ W^{U}\left( z_{i-1},z_{i}\right) \right] ^{H} \cdots ...
...left( z_{i},z_{i-1}\right) \right]^{H} = R\left( z_{i} \right),\end{displaymath}](img148.gif) |
(66) |
or
| ![\begin{displaymath}
\left[ W^{U}\left( z_{i-1},z_{i}\right) \right] ^{H} P\left(...
...left( z_{i},z_{i-1}\right) \right]^{H} = R\left( z_{i} \right).\end{displaymath}](img149.gif) |
(67) |
Defining the cost function as
| 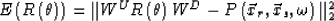 |
(68) |
yields the formula of the linearized migration/inversion:
| ![\begin{displaymath}
R\left( \theta \right) =\frac{\left[ W^{U}\right] ^{H}P\left...
...ft[ W^{U}\right] \left[ W^{D}\right] \left[ W^{D}\right] ^{H}}.\end{displaymath}](img151.gif) |
(69) |
The matrix expression of the migration/inversion in equation (69) is
| ![\begin{eqnarray}
&&\frac{\left[ \begin{array}
{llcl}
\tilde{g}^{U}_{11} & \tilde...
...otfill \\ r_{P1} & r_{P2} & \cdots & r_{PQ} \\ \end{array}\right],\end{eqnarray}](img152.gif) |
|
| (70) |
where the denominator term ![$\left[ M\right] $](img153.gif) is
is
| ![\begin{eqnarray}
\left[ M\right] &=&\left[\begin{array}
{llcl}
\tilde{g}^{D}_{11...
...D}_{Q1} & g^{D}_{Q2} & \cdots & g^{D}_{QN} \\ \end{array}\right] .\end{eqnarray}](img154.gif) |
|
| (71) |
From equation (61) and (70), the migration/inversion can be locally implemented, because all elements in the matrices WU, ![$\left[ W^{U} \right]^{H}$](img144.gif) , WD and
, WD and ![$\left[ W^{D} \right]^{H}$](img145.gif) relate only to a given layer. If the matrix
relate only to a given layer. If the matrix ![$\left[ W^{U} \right]^{H}$](img144.gif) is the inverse of the matrix WU, it can be expressed as
is the inverse of the matrix WU, it can be expressed as
| ![\begin{displaymath}
\left[ W^{U}\right] ^{H}W^{U}=E ,\end{displaymath}](img155.gif) |
(72) |
where the matrix E is an identity matrix. Similarly, if the matrix ![$\left[ W^{D} \right]^{H}$](img145.gif) is the inverse of the matrix WD, we have
is the inverse of the matrix WD, we have
| ![\begin{displaymath}
W^{D}\left[ W^{D}\right] ^{H}=E.\end{displaymath}](img156.gif) |
(73) |
In practice, ![$\left[ W^{U} \right]^{H}$](img144.gif) and
and ![$\left[ W^{D} \right]^{H}$](img145.gif) are the conjugates of WUand WD respectively. Therefore, the matrix
are the conjugates of WUand WD respectively. Therefore, the matrix ![$\left[ M\right] $](img153.gif) is a band-width-limited diagonal matrix.
The velocity structure and the acquisition geometry affect the inner structure of the matrix. In fact, M is a Hessian which will be discussed in detail later.
is a band-width-limited diagonal matrix.
The velocity structure and the acquisition geometry affect the inner structure of the matrix. In fact, M is a Hessian which will be discussed in detail later.





Next: [3] The meaning and
Up: Aspects of Linearized migration/inversion
Previous: [1] Numerical calculation of
Stanford Exploration Project
11/1/2005
![\begin{displaymath}
W^{U}R\left(\theta \right)W^{D} =\left[ \begin{array}
{llcl}...
..._{Q1} & g^{D}_{Q2} & \cdots & g^{D}_{QN} \\ \end{array}\right],\end{displaymath}](img133.gif)
![\begin{displaymath}
W^{U}R\left(\theta \right)W^{D} =\left[ \begin{array}
{llcl}...
..._{Q1} & g^{D}_{Q2} & \cdots & g^{D}_{QN} \\ \end{array}\right],\end{displaymath}](img133.gif)
![\begin{displaymath}
P\left(\vec{x}_{r},\vec{x}_{s},\omega \right) =\sum\limits_{...
... \left( g^{U}rg^{D}\right) _{MN} \\ \end{array}\right]_{i_{z}}.\end{displaymath}](img135.gif)
![\begin{eqnarray}
&&\left[ \begin{array}
{llcl}
\tilde{g}^{U}_{11} & \tilde{g}^{U...
...otfill \\ r_{P1} & r_{P2} & \cdots & r_{PQ} \\ \end{array}\right],\end{eqnarray}](img137.gif)
![\begin{displaymath}
R\left( \theta \right) =\frac{\left[ W^{U}\right] ^{H}P\left...
...ft[ W^{U}\right] \left[ W^{D}\right] \left[ W^{D}\right] ^{H}}.\end{displaymath}](img151.gif)
![\begin{eqnarray}
&&\frac{\left[ \begin{array}
{llcl}
\tilde{g}^{U}_{11} & \tilde...
...otfill \\ r_{P1} & r_{P2} & \cdots & r_{PQ} \\ \end{array}\right],\end{eqnarray}](img152.gif)
![\begin{eqnarray}
\left[ M\right] &=&\left[\begin{array}
{llcl}
\tilde{g}^{D}_{11...
...D}_{Q1} & g^{D}_{Q2} & \cdots & g^{D}_{QN} \\ \end{array}\right] .\end{eqnarray}](img154.gif)