RMO function with arbitrary scaling of velocity

The expressions of the derivative of $z_\gamma$ with respect to arbitrary perturbations of individual velocity components (i.e. V_V, V_H, and V_N) are slightly more complex than with respect to because the wavefronts are deformed when the velocity components are unevenly perturbed. These derivatives can be expressed as:

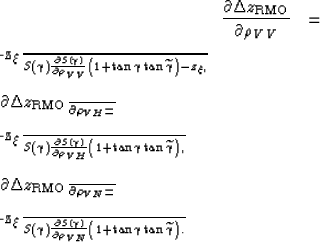
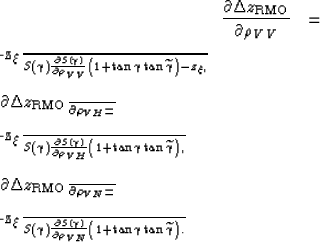$$\begin{eqnarray} \frac{\partial z_\gamma}{\partial \rho_V_V} &=& -\frac{z_\xi}{... ...al \rho_V_N} \left(1 + \tan \gamma\tan \widetilde{\gamma}\right).\end{eqnarray}$$ (21) (22) (23)

The partial derivatives of the RMO function $\Delta z_{\rm RMO}$are directly derived from the partial derivatives of $z_\gamma$, taking into account that for flat reflectors only the vertical velocity component V_V influences the image depth of normal incidence. The derivatives of $\Delta z_{\rm RMO}$ can thus be written as follows:

$$\begin{eqnarray} \frac{\partial \Delta z_{\rm RMO}}{\partial \rho_V_V} &=& -\fr... ...al \rho_V_N} \left(1 + \tan \gamma\tan \widetilde{\gamma}\right).\end{eqnarray}$$ (24) (25) (26)

The expressions for the derivatives of the slowness function with respect to the perturbation parameters depend on the particular form chosen to approximate the slowness function. Appendix C presents a particular approximation to the VTI group slowness function and derives the corresponding partial derivatives to be substituted in equations 21-23 and in equations 24-26. I used the same approximation to the VTI group slowness for the numerical experiments shown in this paper.