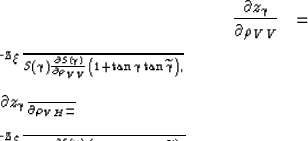Next: RMO function with arbitrary
Up: Anisotropic residual moveout for
Previous: Anisotropic residual moveout for
In case of uniform scaling of velocity,
the derivative of the imaging depth 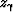 with respect to the perturbation component has the following simple form:
with respect to the perturbation component has the following simple form:
|  |
(18) |
because the derivative of the slowness with respect to
a uniform scaling of the velocity has the following simple form:
| 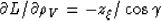 |
(19) |
that causes the derivative
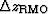 to be independent from the ``local'' shape of the anisotropic slowness function.
Intuitively, this simplification is related to the fact
that the ``shape'' of the wavefronts is not affected
by a uniform scaling of the velocity.
to be independent from the ``local'' shape of the anisotropic slowness function.
Intuitively, this simplification is related to the fact
that the ``shape'' of the wavefronts is not affected
by a uniform scaling of the velocity.
The residual moveout 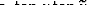 is defined as the difference
between the reflector movement at finite aperture angle
is defined as the difference
between the reflector movement at finite aperture angle 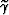 and the reflector movement at normal incidence.
From equation 18 the partial derivative
of
and the reflector movement at normal incidence.
From equation 18 the partial derivative
of 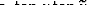 with respect to is equal to the
following expression:
with respect to is equal to the
following expression:
| 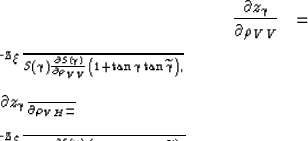 |
(20) |
When the medium is isotropic, and the
phase angles are equal to the group angles,
the RMO expression in equation 20
becomes the RMO expression introduced
by Biondi and Symes (2003).
The dependency of equation 20
from the group angles increases the complexity of its use
because it requires the transformation
of phase angles (measured directly from the ADCIGs)
into group angles by applying equation 31.
The computational cost of evaluating equation 31
is negligible, but its use makes the computations
dependent on the local values of the background
anisotropic velocity function.
On the other hand, the following numerical examples show that
substantial errors are introduced when
the distinction between the group and phase angles
is neglected,
and the phase angle is used instead of the group
angle in equation 20.





Next: RMO function with arbitrary
Up: Anisotropic residual moveout for
Previous: Anisotropic residual moveout for
Stanford Exploration Project
11/1/2005


![]() is defined as the difference
between the reflector movement at finite aperture angle
is defined as the difference
between the reflector movement at finite aperture angle ![]() and the reflector movement at normal incidence.
From equation 18 the partial derivative
of
and the reflector movement at normal incidence.
From equation 18 the partial derivative
of ![]() with respect to is equal to the
following expression:
with respect to is equal to the
following expression: