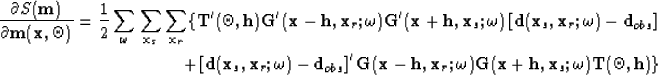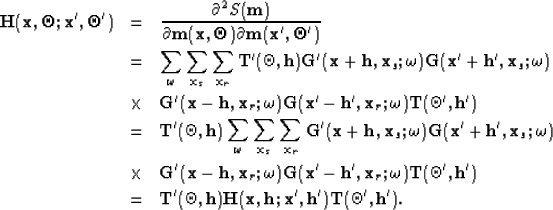Next: Explicit vs. implicit Hessian
Up: Expanding Hessian dimensionality
Previous: Subsurface-offset Hessian
Sava and Fomel (2003) define an image space transformation from subsurface offset to reflection and azimuth angle as:
| 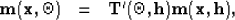 |
(12) |
where 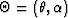 are the reflection and the azimuth angles, and
are the reflection and the azimuth angles, and 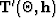 is the adjoint of the angle-to-offset transformation operator (slant stack).
is the adjoint of the angle-to-offset transformation operator (slant stack).
Substituting the prestack migration image (subsurface offset domain) in equation 7 into equation 12 we obtain the expression for the prestack migration image in the angle-domain that follows:
| 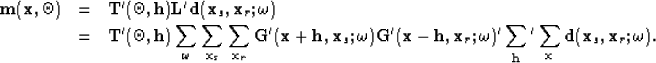 |
(13) |
| |
The synthetic data can be modeled (as the adjoint of equation 14) by the chain of linear operator 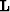 and the angle-to-offset transformation operator acting on the model space,
and the angle-to-offset transformation operator acting on the model space,
| 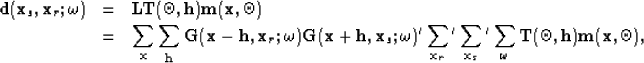 |
|
| (14) |
The quadratic cost function is
| ![\begin{eqnarray}
S({\bf m}) &=& \frac{1}{2} \sum_{\omega}\sum_{{\bf x}_s}\sum_{{...
...\left[ {\bf d}({\bf x}_s,{\bf x}_r;\omega)-{\bf d}_{obs} \right],
\end{eqnarray}](img41.gif) |
|
| (15) |
while its first derivative with respect to the model parameters 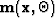 is
is
| 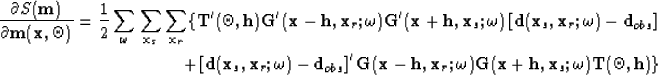 |
|
| (16) |
and its second derivative with respect to the model parameters 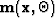 and
and 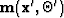 is the angle-domain Hessian
is the angle-domain Hessian
| 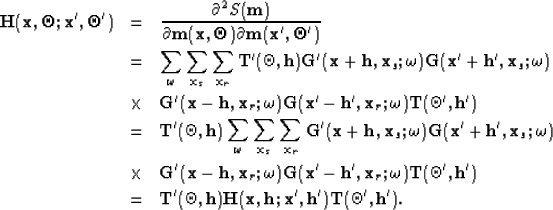 |
|
| |
| |
| |
| |
| (17) |





Next: Explicit vs. implicit Hessian
Up: Expanding Hessian dimensionality
Previous: Subsurface-offset Hessian
Stanford Exploration Project
10/31/2005
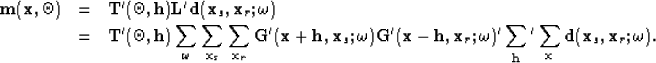
![]() and the angle-to-offset transformation operator acting on the model space,
and the angle-to-offset transformation operator acting on the model space,
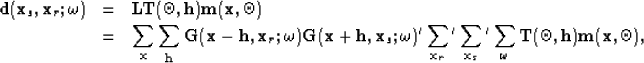
![\begin{eqnarray}
S({\bf m}) &=& \frac{1}{2} \sum_{\omega}\sum_{{\bf x}_s}\sum_{{...
...\left[ {\bf d}({\bf x}_s,{\bf x}_r;\omega)-{\bf d}_{obs} \right],
\end{eqnarray}](img41.gif)