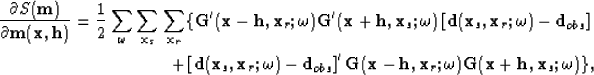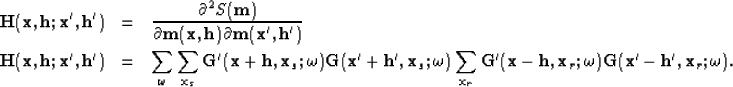Next: Angle-domain Hessian
Up: Expanding Hessian dimensionality
Previous: Expanding Hessian dimensionality
The prestack migration image (subsurface offset domain) for a group of shots positioned at 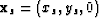 and a group of receivers positioned at
and a group of receivers positioned at 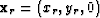 can be given by the adjoint of a linear operator
can be given by the adjoint of a linear operator 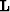 acting on the data-space
acting on the data-space 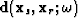 as
as
| 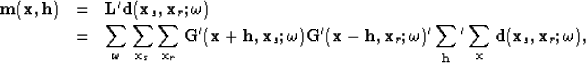 |
|
| (7) |
where 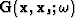 and
and 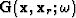 are the Green functions from shot position
are the Green functions from shot position 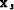 and receiver position
and receiver position 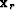 to a model space point
to a model space point 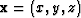 , and
, and 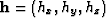 is the subsurface offset. The symbols
is the subsurface offset. The symbols 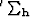 and
and 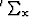 are spray (adjoint of the sum) operators in the subsurface offset and model space dimensions, respectively.
are spray (adjoint of the sum) operators in the subsurface offset and model space dimensions, respectively.
The synthetic data can be modeled (as the adjoint of equation 7) by the linear operator 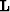 acting on the model space
acting on the model space 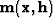 with
with 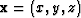 and
and 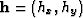
| 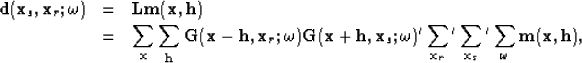 |
|
| (8) |
where the symbols 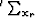 ,
,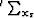 , and
, and 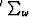 are spray operators in the shot, receiver, and frequency dimensions, respectively.
are spray operators in the shot, receiver, and frequency dimensions, respectively.
In equations 7 and 8 the Green functions are computed by means of the one-way wave equation Ehinger et al. (1996) and the extrapolation is performed using the adequate paraxial wave equations (flux conservation) Bamberger et al. (1988).
The quadratic cost function is
| ![\begin{eqnarray}
S({\bf m}) &=& \frac{1}{2} \sum_{\omega}\sum_{{\bf x}_s}\sum_{{...
...f d}({\bf x}_s,{\bf x}_r;\omega)-{\bf d}_{obs} \right], \nonumber
\end{eqnarray}](img33.gif) |
(9) |
| |
while its first derivative, with respect to the model parameters 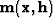 , is
, is
| 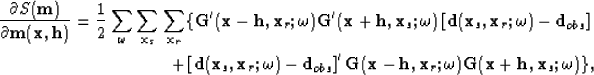 |
|
| (10) |
and its second derivative with respect to the model parameters 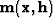 and
and 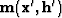 is the subsurface offset Hessian:
is the subsurface offset Hessian:
| 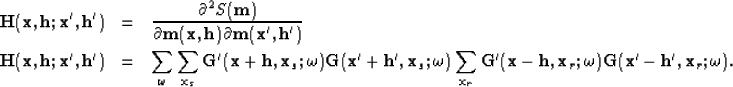 |
(11) |
| |
The next subsection shows how to go from subsurface offset to reflection and azimuth angle dimensions following the Sava and Fomel (2003) approach.





Next: Angle-domain Hessian
Up: Expanding Hessian dimensionality
Previous: Expanding Hessian dimensionality
Stanford Exploration Project
10/31/2005
![]() and a group of receivers positioned at
and a group of receivers positioned at ![]() can be given by the adjoint of a linear operator
can be given by the adjoint of a linear operator ![]() acting on the data-space
acting on the data-space ![]() as
as
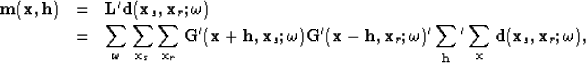
![]() acting on the model space
acting on the model space ![]() with
with ![]() and
and ![]()
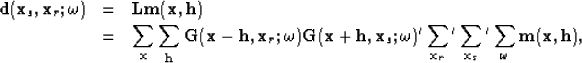
![\begin{eqnarray}
S({\bf m}) &=& \frac{1}{2} \sum_{\omega}\sum_{{\bf x}_s}\sum_{{...
...f d}({\bf x}_s,{\bf x}_r;\omega)-{\bf d}_{obs} \right], \nonumber
\end{eqnarray}](img33.gif)