




Next: POROELASTICITY ESTIMATES AND BOUNDS
Up: BOUNDS ON ELASTIC CONSTANTS
Previous: Voigt and Reuss Bounds
It has been shown elsewhere (Berryman, 2004a,b)
that the Peselnick-Meister-Watt
bounds for bulk modulus of a random polycrystal composed of
hexagonal (or transversely isotropic) grains are given by
| 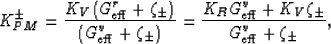 |
(10) |
where 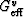 (
(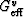 ) is the uniaxial shear energy per
unit volume for a unit applied shear strain (stress).
The second equality follows directly from the product formula
(9). Parameters
) is the uniaxial shear energy per
unit volume for a unit applied shear strain (stress).
The second equality follows directly from the product formula
(9). Parameters 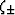 are defined by
are defined by
| 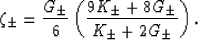 |
(11) |
In (11), values of 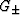 (shear moduli of isotropic
comparison materials) are determined by inequalities
(shear moduli of isotropic
comparison materials) are determined by inequalities
| 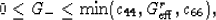 |
(12) |
and
| 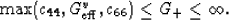 |
(13) |
The values of 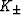 (bulk moduli of isotropic
comparison materials) are then determined by equalities
(bulk moduli of isotropic
comparison materials) are then determined by equalities
| 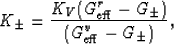 |
(14) |
given by Peselnick and Meister (1965) and Watt and Peselnick (1980). Also see Berryman, 2004b).
Bounds on the shear moduli are then given by
| ![\begin{displaymath}
\begin{array}
{r}
\frac{1}{\mu_{\rm hex}^\pm + \zeta_\pm} = ...
..._{44}+\zeta_\pm} + \frac{2}{c_{66}+\zeta_\pm}\big],\end{array} \end{displaymath}](img34.gif) |
(15) |
where 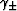 and
and 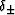 are given by
are given by
| ![\begin{displaymath}
\gamma_\pm = \frac{-1}{K_\pm + 4G_\pm/3} \qquad\hbox{and}\qq...
... \left[\frac{4}{15}
- \frac{2}{5G_\pm\gamma_\pm}\right]^{-1}.
\end{displaymath}](img37.gif) |
(16) |
KV is the Voigt average of the bulk modulus as defined previously.





Next: POROELASTICITY ESTIMATES AND BOUNDS
Up: BOUNDS ON ELASTIC CONSTANTS
Previous: Voigt and Reuss Bounds
Stanford Exploration Project
5/3/2005
![\begin{displaymath}
\begin{array}
{r}
\frac{1}{\mu_{\rm hex}^\pm + \zeta_\pm} = ...
..._{44}+\zeta_\pm} + \frac{2}{c_{66}+\zeta_\pm}\big],\end{array} \end{displaymath}](img34.gif)