




Next: Hashin-Shtrikman Bounds
Up: BOUNDS ON ELASTIC CONSTANTS
Previous: BOUNDS ON ELASTIC CONSTANTS
For hexagonal symmetry, the nonzero stiffness constants are:
c11, c12, c13 = c23, c33, c44 = c55, and
c66 = (c11-c12)/2.
The Voigt average (Voigt, 1928) for bulk modulus of hexagonal systems is well-known to be
| ![\begin{displaymath}
K_V = \left[2(c_{11}+c_{12}) +4c_{13}+c_{33}\right]/9.
\end{displaymath}](img14.gif) |
(4) |
Similarly, for the shear modulus we have
| 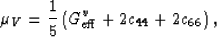 |
(5) |
where the new term appearing here is essentially defined by
(5) and given explicitly by
| 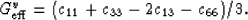 |
(6) |
The quantity 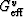 is the energy
per unit volume in a grain when a pure uniaxial shear strain of
unit magnitude [i.e.,
is the energy
per unit volume in a grain when a pure uniaxial shear strain of
unit magnitude [i.e.,
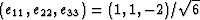 ], whose main compressive
strain is applied to the grain along its axis of symmetry
(Berryman, 2004a,b).
], whose main compressive
strain is applied to the grain along its axis of symmetry
(Berryman, 2004a,b).
The Reuss average (Reuss, 1929) KR for bulk modulus can also be written
in terms of stiffness coefficients as
| 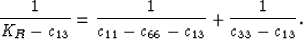 |
(7) |
The Reuss average for shear is
| ![\begin{displaymath}
\mu_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^r} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img20.gif) |
(8) |
which again may be taken as the definition of 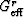 -
i.e., the energy per unit volume in a grain when a pure uniaxial
shear stress of unit magnitude [i.e.,
-
i.e., the energy per unit volume in a grain when a pure uniaxial
shear stress of unit magnitude [i.e.,
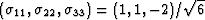 ],
whose main compressive pressure is applied to a grain along
its axis of symmetry.
],
whose main compressive pressure is applied to a grain along
its axis of symmetry.
For each grain having hexagonal symmetry, two product formulas hold
(Berryman, 2004a): 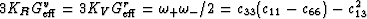 .The symbols
.The symbols 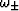 stand for the quasi-compressional and
quasi-uniaxial-shear eigenvalues for the crystalline grains.
Thus, it follows that
stand for the quasi-compressional and
quasi-uniaxial-shear eigenvalues for the crystalline grains.
Thus, it follows that
| 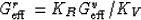 |
(9) |
is a general formula, valid for hexagonal symmetry. We can choose
to treat (5) and (8) as the fundamental
defining equations for 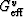 and
and 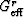 ,respectively.
Equivalently, we can use (9) as the definition
of
,respectively.
Equivalently, we can use (9) as the definition
of 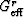 .
.





Next: Hashin-Shtrikman Bounds
Up: BOUNDS ON ELASTIC CONSTANTS
Previous: BOUNDS ON ELASTIC CONSTANTS
Stanford Exploration Project
5/3/2005
![\begin{displaymath}
\mu_R = \left[\frac{1}{5}\left(\frac{1}{G_{\rm eff}^r} + \frac{2}{c_{44}}
+ \frac{2}{c_{66}}\right)\right]^{-1},
\end{displaymath}](img20.gif)
![]() .The symbols
.The symbols ![]() stand for the quasi-compressional and
quasi-uniaxial-shear eigenvalues for the crystalline grains.
Thus, it follows that
stand for the quasi-compressional and
quasi-uniaxial-shear eigenvalues for the crystalline grains.
Thus, it follows that