




Next: Results
Up: Adjoint Implementation
Previous: Adjoint Implementation
There are several issues that must be considered when implementing AMO in this form.
The large volume of data that we are dealing with means that the problem
must be parallelized.
The problem can be parallelized in several different ways.
While it is possible to split in the (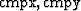 ) plane, boundary
effect are a concern because
the operator is applied in the wave-number domain.
Because the operator is applied in the frequency
domain parallelizing over frequency seems a natural choice.
The problem with dividing the problem along the frequency axis
is that the intermediate
space
) plane, boundary
effect are a concern because
the operator is applied in the wave-number domain.
Because the operator is applied in the frequency
domain parallelizing over frequency seems a natural choice.
The problem with dividing the problem along the frequency axis
is that the intermediate
space  can become enormous, even for fairly small datasets,
which would require some level of patching along other axes. In addition
it requires a troubling transpose. The input data has its
inner axis as time, while we want the outer axis to be frequency.
For multi-gigabyte this can be quite time consuming.
For this reason
I chose to parallelize offset.
Each process is assigned an output (hx,hy) range.
It takes the input that range plus
the additional summation range
implied by equation (2).
can become enormous, even for fairly small datasets,
which would require some level of patching along other axes. In addition
it requires a troubling transpose. The input data has its
inner axis as time, while we want the outer axis to be frequency.
For multi-gigabyte this can be quite time consuming.
For this reason
I chose to parallelize offset.
Each process is assigned an output (hx,hy) range.
It takes the input that range plus
the additional summation range
implied by equation (2).
The parallel job is controlled by the library described
in Clapp (2005).
Each node receives a SEP3D Biondi et al. (1996) volume corresponding
to its output space and the summation region implied
by (2).
The serial code first NMOs, log-stretches, and converts
to frequency its data volume. The data volume is transposed and
equation (6) is applied. The regularized
frequency slices are transposed, inverse Fourier transformed,
and has inverse NMO applied to it. Finally
the data is recombined to form the regularized volume.





Next: Results
Up: Adjoint Implementation
Previous: Adjoint Implementation
Stanford Exploration Project
5/3/2005