Arbitrary scaling of velocity

The expressions of the derivative of $z_\gamma$ with respect to arbitrary perturbations of individual velocity components (i.e. V_V, V_H, and V_N) are slightly more complex than with respect to because the wavefronts are deformed when the velocity components are unevenly perturbed. These derivatives can be expressed as:

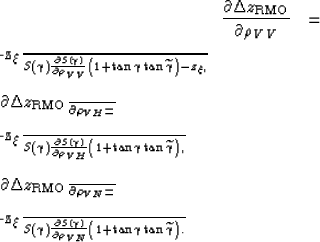
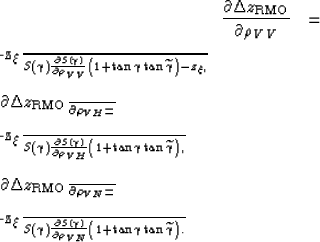$$\begin{eqnarray} \frac{\partial z_\gamma}{\partial \rho_V_V} &=& -\frac{z_\xi}{... ...al \rho_V_N} \left(1 + \tan \gamma\tan \widetilde{\gamma}\right).\end{eqnarray}$$ (40) (41) (42)

The expressions for the derivatives of the slowness function with respect to the perturbation parameters depend on the particular form chosen to approximate the slowness function. Appendix C derives these derivative for the VTI group slowness function approximation expressed in equation 6, which I used for the numerical experiments shown in this paper.

The partial derivatives of the RMO function $\Delta z_{\rm RMO}$are directly derived from the partial derivatives of $z_\gamma$, taking into account that for flat reflectors only the vertical velocity component V_V influences the image depth of normal incidence. The derivatives of $\Delta z_{\rm RMO}$ can thus be written as follows:

$$\begin{eqnarray} \frac{\partial \Delta z_{\rm RMO}}{\partial \rho_V_V} &=& -\fr... ...al \rho_V_N} \left(1 + \tan \gamma\tan \widetilde{\gamma}\right).\end{eqnarray}$$ (43) (44) (45)

Figures  and  show examples of the application of the generalized RMO functions expressed in equations 44-46. As in Figures - , I show the ADCIGs for three different anisotropic rock types, but, differently from the previous figures, not for the isotropic case. The order of the rock types is the same as in Figures - ; that is: panels a) correspond to Taylor Sand, panels b) to Mesa Clay Shale, and panels c) to GreenLight River Shale. Furthermore, as in Figures - , one figure (Figure ) shows the ADCIG obtained with a smaller perturbation than the ADCIGs shown in the other figure (Figure ). The ADCIGs shown in Figure  were obtained by performing isotropic migration on the synthetic data modeled assuming anisotropic velocity. 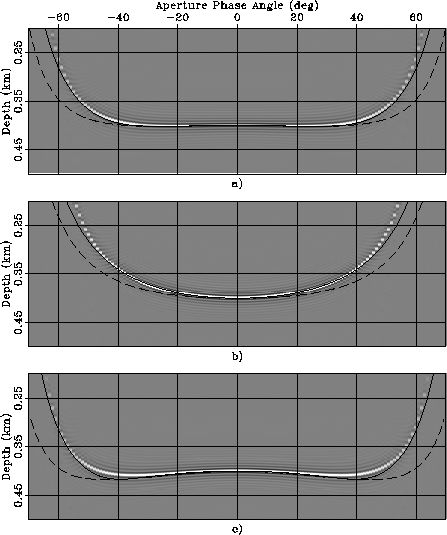The ADCIGs shown in Figure  were computed by scaling by .25 the parameter perturbations used to compute Figure . The lines superimposed onto the images are the RMO functions computed by using the correct values for $\tan \gamma$ (solid lines), and by using $\tan \widetilde{\gamma}$ in place of $\tan \gamma$ (dashed lines).

The predicted RMO functions accurately track the actual RMO functions when the parameter perturbations are sufficiently small to be within the range of accuracy of the linearization at the basis of the derivation of equation 40 (Figure ). But even when the perturbations are large (Figure ) and cause a substantial RMO (up to 30% of the reflector depth) the predicted RMO functions are excellent approximations of the actual RMO functions.

The RMO functions associated with the two strongly unelliptical rocks (Taylor Sand and GreenLight River Shale) exhibit a characteristic oscillatory behavior; the events at narrow-aperture angles are imaged deeper than the normal incidence event, whereas the events at wide-aperture angles are imaged shallower. This oscillatory behavior is well predicted by the analytical RMO function introduced in equations 44-46.

In contrast, the approximation of the group angles with the phase angles (dashed lines in the figures) seriously deteriorates the accuracy of the predicted RMO functions. Notice that, in contrast with the uniform perturbation case illustrated in Figures - , the dashed lines are different among the panels, because the derivatives of the slowness function with respect to the perturbation parameters depend on the anisotropic parameters of the background medium.

 

Trio_Aniso-iso_overn
Figure 9 ADCIGs obtained when data modeled with an anisotropic velocity have been migrated using an isotropic velocity. The anisotropic data were modeled assuming three rock types: a) Taylor Sand, b) Mesa Clay Shale, and c) GreenLight River Shale. Superimposed onto the images are the RMO functions computed using equation 40. The solid line was computed when $\tan \gamma$ was derived from $\tan \widetilde{\gamma}$by applying equation 1, whereas the dashed line was computed by approximating $\tan \gamma$ as equal to $\tan \widetilde{\gamma}$.

 

Trio_Aniso-scaled_overn
Figure 10 ADCIGs obtained when data modeled with an anisotropic velocity have been migrated using a less anisotropic velocity; that is, with anisotropic parameters obtained by scaling by .25 the parameter perturbations used to compute Figure . The anisotropic data were modeled assuming three rock types: a) Taylor Sand, b) Mesa Clay Shale, and c) GreenLight River Shale. Superimposed onto the images are the RMO functions computed using equation 40. The solid line was computed when $\tan \gamma$ was derived from $\tan \widetilde{\gamma}$by applying equation 1, whereas the dashed line was computed by approximating $\tan \gamma$ as equal to $\tan \widetilde{\gamma}$.