Conversion of depth errors into traveltime errors

The RMO functions derived above can be directly used in a layered-based vertical updating of the velocity function after migration. However, in complex media it is often desirable to invert the depth errors measured from ADCIGs into velocity-parameters perturbations through a tomographic procedure. To be able to apply a tomographic method, we must perform an additional step to convert the depth errors measured from ADCIGs into traveltime errors. This depth-to-time conversion can be easily accomplished by slightly rewriting the chain of partial derivatives in equation 35, and obtain the following relationship:  

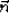$$\frac{\partial z_\gamma}{\partial t} = \frac{\partial z_\gam... ...mma+ \sin \gamma\tan \widetilde{\gamma}}{S\left(\gamma\right)},$$ (46)

which can be directly applied to convert depth errors into traveltime perturbations to be used in tomography.