




Next: Angles of departure and
Up: Liner and Vlad: Multiple
Previous: Computing the traveltime: the
We will illustrate the theory presented above using the multiple
reflection event S1010201G (the zeros denote the Earth surface). For
this event, n=6, 1 less than the total number of bounces in
the earth. The first step is generating sequences 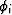 and li, according
to (5) and (6):
and li, according
to (5) and (6):
| 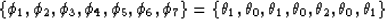 |
(39) |
and
| 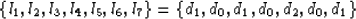 |
(40) |
We prepend
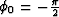 to the
sequence of angles, then we compute the
to the
sequence of angles, then we compute the 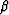 sequence:
sequence:
| 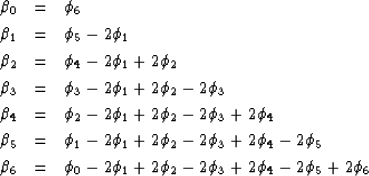 |
(41) |
| (42) |
| (43) |
| (44) |
| (45) |
| (46) |
| (47) |
It may be useful to notice the regularities in signs and indices. The
summation and trigonometric operators in (25) and (26)
can be written in matrix form to verify the correctness of their numerical
implementation. We then
compute the auxiliary vectors given by (29) and (33):
| ![\begin{displaymath}
\begin{array}
{l}
{\bf u}_1 =
\frac{2}{v}l_5\left[ {\begin{...
...i_7} \\ {-\cos\phi_7}
\\ \end{array}} \right] \\ \end{array},\end{displaymath}](img55.gif) |
(48) |
| ![\begin{displaymath}
{\bf u}_4=\frac{1}{v}\left[
{\begin{array}
{*{20}c}{\sin\le...
...cos\left(-\beta_6\right)+\sin2\phi_7}
\\ \end{array}} \right],\end{displaymath}](img56.gif) |
(49) |
For our very particular case in which some of the bounces are with the
surface (d0=0, 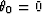 ),
),
| ![\begin{displaymath}
{\bf u}_1 = \frac{2}{v}
d_1\left[
{\begin{array}
{*{20}c}{+...
...-\cos\left(2\theta_1-\theta_2\right)}
\\ \end{array}} \right],\end{displaymath}](img58.gif) |
(50) |
| ![\begin{displaymath}
{\bf u}_4=\frac{2}{v}\cos\left(3\theta_1+\theta_2\right)
\le...
...{-\sin\left(\theta_1+\theta_2\right)}
\\ \end{array}} \right],\end{displaymath}](img59.gif) |
(51) |
and the traveltime for each offset h can now be computed by plugging
these vectors directly into (35).
By performing trigonometric operations, we may find that the expression for the
distance is the same as that in Equation (A-14) of
Levin and Shah (1977).





Next: Angles of departure and
Up: Liner and Vlad: Multiple
Previous: Computing the traveltime: the
Stanford Exploration Project
10/23/2004
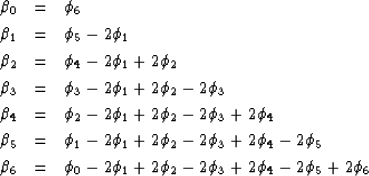
![\begin{displaymath}
\begin{array}
{l}
{\bf u}_1 =
\frac{2}{v}l_5\left[ {\begin{...
...i_7} \\ {-\cos\phi_7}
\\ \end{array}} \right] \\ \end{array},\end{displaymath}](img55.gif)