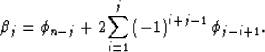Next: Computing the traveltime: the
Up: Liner and Vlad: Multiple
Previous: Problem setup
In order to compute the position of the image after a cascade of
several image-construction operations, we first need to define the
cascade sequence c as the ordered sequence of interface numbers at
which we will consider that a reflection occurs. We define the source
as S(-h,0) and the receiver as G(0,h), as shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Because both S and G are at the surface,
any sort of multiple event will be reflected more than once by the
same interface. Therefore, the mapping of
the counting index i of the cascading sequence onto the values
ci of the cascading sequence is therefore surjective, but not
injective. To be able to work with indices in an efficient manner, we
describe the geometry of the problem through the sequences
. Because both S and G are at the surface,
any sort of multiple event will be reflected more than once by the
same interface. Therefore, the mapping of
the counting index i of the cascading sequence onto the values
ci of the cascading sequence is therefore surjective, but not
injective. To be able to work with indices in an efficient manner, we
describe the geometry of the problem through the sequences
| 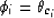 |
(5) |
and
which incorporate information both on the geometry of the interfaces
and on the order of the cascade, and for which the index numbering
starts with the value 1. The subscripts for q will also
denote the counting index for the image reflection cascade. The first
reflection operation can be written as
| 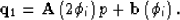 |
(7) |
Then,
| 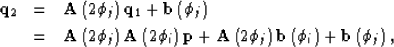 |
(8) |
| (9) |
| 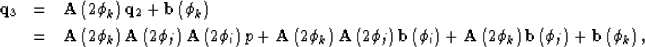 |
(10) |
| (11) |
and so on. Let us denote the counterclockwise rotation matrix with
| ![\begin{displaymath}
{\bf R}\left(\alpha\right) = \left[ {\begin{array}
{*{20}c}
...
...} \\ {\sin \alpha } & { \cos \alpha } \\ \end{array}} \right].\end{displaymath}](img12.gif) |
(12) |
Both 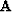 and
and 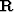 are involutory matrices. It can be easily verified that:
are involutory matrices. It can be easily verified that:
| 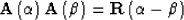 |
(13) |
| 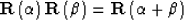 |
(14) |
| 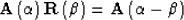 |
(15) |
| 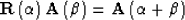 |
(16) |
Chains of 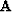 operators can be written as a single operator:
operators can be written as a single operator:
| 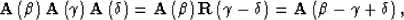 |
(17) |
| 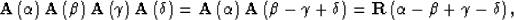 |
(18) |
According to (15), we can write any 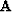 as
as
| ![\begin{displaymath}
{\bf A} \left( \alpha \right) = \left[ {\begin{array}
{*{20}...
...& {-1} \\ \end{array}} \right] {\bf R} \left( - \alpha
\right),\end{displaymath}](img21.gif) |
(19) |
so the product of any number k of 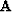 operators can be written as
operators can be written as
| 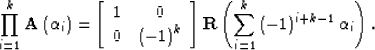 |
(20) |
To use these properties for constructing
cascades of image reflections, we must replace the set 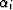 with
the inverse succession of the dips of the reflecting interfaces,
multiplied by two according to the definition of
with
the inverse succession of the dips of the reflecting interfaces,
multiplied by two according to the definition of 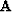 in (4):
in (4):
| 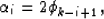 |
(21) |
where 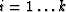 . The reverse ``chronological'' order is a consequence of the operators
in the chain being matrices that multiply the previous image
coordinate vector from the left, as exemplified by (8) and
(10). The result
of the succession of image-building operations can be written as
. The reverse ``chronological'' order is a consequence of the operators
in the chain being matrices that multiply the previous image
coordinate vector from the left, as exemplified by (8) and
(10). The result
of the succession of image-building operations can be written as
| 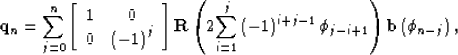 |
(22) |
where we define a nonphysical quantity 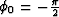 and we
also define
and we
also define 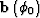 as the coordinates vector of
the initial point in the cascade of reflections. We also consider that the
summation index increases in increments of 1 and that summation
operators return zero when the upper summation limit is smaller than
the lower summation limit. Under the assumption that the starting
point of the cascade is at the surface, and by denoting half of
its x coordinate with l0, we can write all
as the coordinates vector of
the initial point in the cascade of reflections. We also consider that the
summation index increases in increments of 1 and that summation
operators return zero when the upper summation limit is smaller than
the lower summation limit. Under the assumption that the starting
point of the cascade is at the surface, and by denoting half of
its x coordinate with l0, we can write all 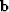 vectors
using rotations:
vectors
using rotations:
| ![\begin{displaymath}
{\bf b}\left( \phi_i\right) = 2 l_i \left[ {\begin{array}
{*...
...[ {\begin{array}
{*{20}c}
{1} \\ {0} \\ \end{array}} \right].\end{displaymath}](img30.gif) |
(23) |
Substituting this into (22),
| ![\begin{displaymath}
{\bf q}_n = 2 \sum\limits_{j=0}^n l_{n-j}\left[ {\begin{arra...
...[ {\begin{array}
{*{20}c}
{1} \\ {0} \\ \end{array}} \right],\end{displaymath}](img31.gif) |
(24) |
These particular choices of l0 and 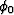 , together with
the assumption of a surface starting point, ensure that
(23) is consistent for the starting point of the cascading
operations too. After a few algebraic manipulations, we obtain
, together with
the assumption of a surface starting point, ensure that
(23) is consistent for the starting point of the cascading
operations too. After a few algebraic manipulations, we obtain
| ![\begin{displaymath}
{\bf q}_n = 2 \sum\limits_{j=0}^n l_{n-j}\left[ {\begin{arra...
..._j} \\ {\left(-1\right)^j \cos\beta_j} \\ \end{array}} \right],\end{displaymath}](img33.gif) |
(25) |
where
| 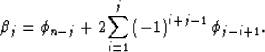 |
(26) |





Next: Computing the traveltime: the
Up: Liner and Vlad: Multiple
Previous: Problem setup
Stanford Exploration Project
10/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Because both S and G are at the surface,
any sort of multiple event will be reflected more than once by the
same interface. Therefore, the mapping of
the counting index i of the cascading sequence onto the values
ci of the cascading sequence is therefore surjective, but not
injective. To be able to work with indices in an efficient manner, we
describe the geometry of the problem through the sequences
. Because both S and G are at the surface,
any sort of multiple event will be reflected more than once by the
same interface. Therefore, the mapping of
the counting index i of the cascading sequence onto the values
ci of the cascading sequence is therefore surjective, but not
injective. To be able to work with indices in an efficient manner, we
describe the geometry of the problem through the sequences
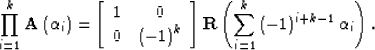
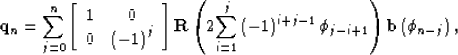
![\begin{displaymath}
{\bf q}_n = 2 \sum\limits_{j=0}^n l_{n-j}\left[ {\begin{arra...
...[ {\begin{array}
{*{20}c}
{1} \\ {0} \\ \end{array}} \right],\end{displaymath}](img31.gif)
![\begin{displaymath}
{\bf q}_n = 2 \sum\limits_{j=0}^n l_{n-j}\left[ {\begin{arra...
..._j} \\ {\left(-1\right)^j \cos\beta_j} \\ \end{array}} \right],\end{displaymath}](img33.gif)