




Next: Conclusion
Up: Liner and Vlad: Multiple
Previous: Computing the traveltime: an
The previous sections presented a method to compute the traveltime
from a given source point to a given receiver point. Using the image point
reflection method has eschewed the need for traditional ray
tracing. However, in order to estimate the effect of the acquisition
arrays on the amplitudes, or to graphically display the raypaths,
we need to compute the angles of departure of the rays from the source
and of arrival to the receiver.
Shah (1973) shows that if we denote with 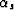 the smallest
angle between the raypath departing from the source and the vertical,
with
the smallest
angle between the raypath departing from the source and the vertical,
with 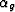 the similarly defined arrival angle, with s the
coordinate of the source and with g the coordinate of the receiver,
the two angles can be found from the relations:
the similarly defined arrival angle, with s the
coordinate of the source and with g the coordinate of the receiver,
the two angles can be found from the relations:
| 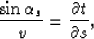 |
(52) |
| 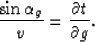 |
(53) |
Writing (32) as
| 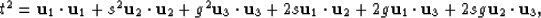 |
(54) |
we obtain
| 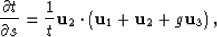 |
(55) |
| 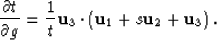 |
(56) |
Replacing now s with -h and g with h, the angles are given by:
| 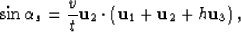 |
(57) |
| 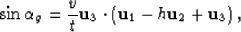 |
(58) |
where t is computed as a function of h as given by (35).





Next: Conclusion
Up: Liner and Vlad: Multiple
Previous: Computing the traveltime: an
Stanford Exploration Project
10/23/2004
![]() the smallest
angle between the raypath departing from the source and the vertical,
with
the smallest
angle between the raypath departing from the source and the vertical,
with ![]() the similarly defined arrival angle, with s the
coordinate of the source and with g the coordinate of the receiver,
the two angles can be found from the relations:
the similarly defined arrival angle, with s the
coordinate of the source and with g the coordinate of the receiver,
the two angles can be found from the relations: