




Next: Numerical examples
Up: Rosales: NHNMO
Previous: Introduction
The main characteristic of converted-wave data is their non-hyperbolic moveout.
However, for certain offset/depth
ratios, it is possible to approximate the non-hyperbolic
moveout as a hyperbola Tessmer and Behle (1988).
Tessmer and Behle (1988) extend the work of Taner and Koehler (1969)
for converted waves. They apply a second-order
approximation to the moveout equation to converted-wave
data. In such cases the stacking velocity corresponds to the product of
both P and S velocities known as converted-wave
velocity.
Castle (1988) presents the third-order-approximation
coefficient terms for the converted-wave moveout equation.
In this note, I simplify this term and present it as a function
of 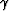 alone.
alone.
Equation (1) is the expanded traveltime function
of reflected PP or SS data presented by Taner and Koehler (1969):
|
t2 = c1 + c2 x2 + c3 x4,
|
(1) |
where x represents full offset, c1 = b12, 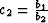 , and
, and
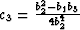 , with
, with
| 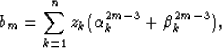 |
(2) |
where k indicates the stratigraphic layers present in the model.
Here and hereafter, 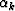 and
and 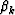 respectively denote the P velocity and
the S velocity for the
respectively denote the P velocity and
the S velocity for the 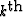 -layer.
Tessmer and Behle (1988) show that
-layer.
Tessmer and Behle (1988) show that
| 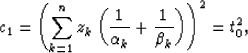 |
(3) |
and
| 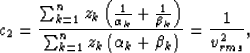 |
(4) |
where 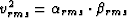 , this is only true when
, this is only true when 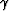 is constant.
The formal definition for c3 is as follows Castle (1988):
is constant.
The formal definition for c3 is as follows Castle (1988):
| 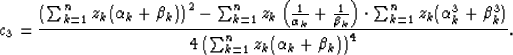 |
(5) |
For one layer, equation (5) simplifies to
| ![\begin{displaymath}
c_3 = \frac{z^2 \left [ (\alpha+\beta)^2 - (\frac{1}{\alpha}...
...{\beta})(\alpha^3 + \beta^3) \right ]}{4 z^4 (\alpha+\beta)^4},\end{displaymath}](img12.gif) |
(6) |
which reduces to
| 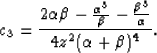 |
(7) |
Now, the simple trick I use to make an educated guess for 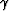 with PS data alone
is to consider [from the results of c1 and c2, equations (3) and (4)]
that
with PS data alone
is to consider [from the results of c1 and c2, equations (3) and (4)]
that 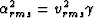 and
and
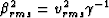 , remember that
, remember that 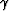 is approximately constant in all layers.
With these assumptions, equation (5) simplifies to
is approximately constant in all layers.
With these assumptions, equation (5) simplifies to
| 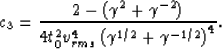 |
(8) |
Introducing the final results for c1, c2 and c3 into equation (1),
I obtain an equation to perform non-hyperbolic moveout for PS data that is
dependent on only two parameters: 1) the multiplication of the P and S velocities, or the
converted wave rms velocity (vrms),
and 2) the Vp/Vs ratio (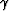 ). It is also important to note that this equation is valid for a
constant Poisson's ratio in all layers. With these simplifications and equations, it is possible to
obtain an approximate value of
). It is also important to note that this equation is valid for a
constant Poisson's ratio in all layers. With these simplifications and equations, it is possible to
obtain an approximate value of 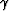 using PS data alone.
using PS data alone.
|
| ![\begin{displaymath}
t^2 = t_0^2 + \frac{x^2}{v_{rms}^2} + \frac{x^4}{t_0^2 v_{rm...
... )}{4 \left( \gamma^{1/2} + \gamma^{-1/2} \right ) ^4} \right ]\end{displaymath}](img17.gif) |
(9) |
|
Equation (9) is the central result of this paper. It is possible to note
that the moveout equation is more than a hyperbolic relation, since it involves a
third term. Another important characteristic of equation (9)
is that it depends only on two parameters: 1) the converted-waves rms velocity, and 2) the
Vp/Vs ratio. This important characteristic will allow us to invert for
a value of 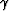 . It is also important to note that the
sensitivity of equation (9) to
. It is also important to note that the
sensitivity of equation (9) to 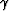 probably is not too high, since the third term
of the equation also depends on the offset-depth ratio.
probably is not too high, since the third term
of the equation also depends on the offset-depth ratio.
It is important to note that for the specific case of 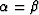 (this never happens in practice),
i.e., no converted waves,
the value of
(this never happens in practice),
i.e., no converted waves,
the value of 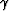 equals 1, and equation (9) reduces to the conventional normal moveout
equation. This is also a result of the one layer assumption.
equals 1, and equation (9) reduces to the conventional normal moveout
equation. This is also a result of the one layer assumption.





Next: Numerical examples
Up: Rosales: NHNMO
Previous: Introduction
Stanford Exploration Project
10/23/2004
![]() alone.
alone.
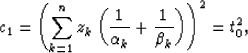
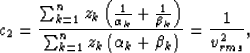
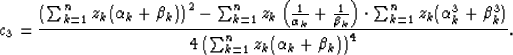
![\begin{displaymath}
c_3 = \frac{z^2 \left [ (\alpha+\beta)^2 - (\frac{1}{\alpha}...
...{\beta})(\alpha^3 + \beta^3) \right ]}{4 z^4 (\alpha+\beta)^4},\end{displaymath}](img12.gif)
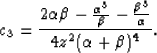
![]() . It is also important to note that the
sensitivity of equation (9) to
. It is also important to note that the
sensitivity of equation (9) to ![]() probably is not too high, since the third term
of the equation also depends on the offset-depth ratio.
probably is not too high, since the third term
of the equation also depends on the offset-depth ratio.
![]() (this never happens in practice),
i.e., no converted waves,
the value of
(this never happens in practice),
i.e., no converted waves,
the value of ![]() equals 1, and equation (9) reduces to the conventional normal moveout
equation. This is also a result of the one layer assumption.
equals 1, and equation (9) reduces to the conventional normal moveout
equation. This is also a result of the one layer assumption.