Next: Conclusions and Future Work
Up: Rosales: NHNMO
Previous: Theory: Non-hyperbolic moveout
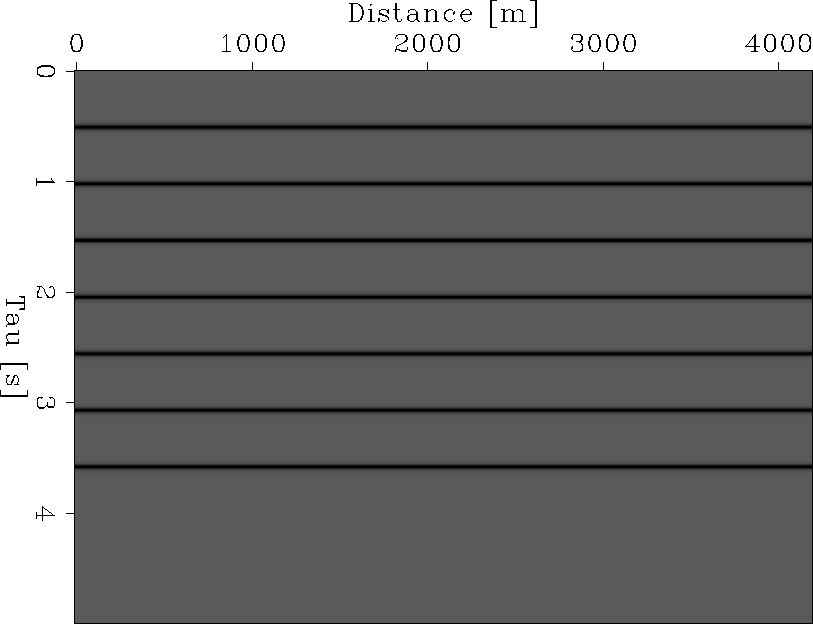
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents a simple flat-layer model. Figures
presents a simple flat-layer model. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the result of modeling the two-way travel time with the conventional normal
moveout equation, and
with the non-hyperbolic moveout equation, using an initial velocity of 1100 m/s, a velocity
gradient of 125
show the result of modeling the two-way travel time with the conventional normal
moveout equation, and
with the non-hyperbolic moveout equation, using an initial velocity of 1100 m/s, a velocity
gradient of 125 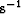 and a constant value of
and a constant value of 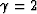 .
.
Both results (Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) present a hyperbolic moveout at
near offset or small offset-to-depth ratio. This result resembles the well known theoretical
presentation of
Tessmer and Behle (1988). However, the non-hyperbolic moveout is dominant for large offsets
and shallow depths, as
can be observed in Figure
) present a hyperbolic moveout at
near offset or small offset-to-depth ratio. This result resembles the well known theoretical
presentation of
Tessmer and Behle (1988). However, the non-hyperbolic moveout is dominant for large offsets
and shallow depths, as
can be observed in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
mod5
Figure 1 Reflectivity model.
|
|  |





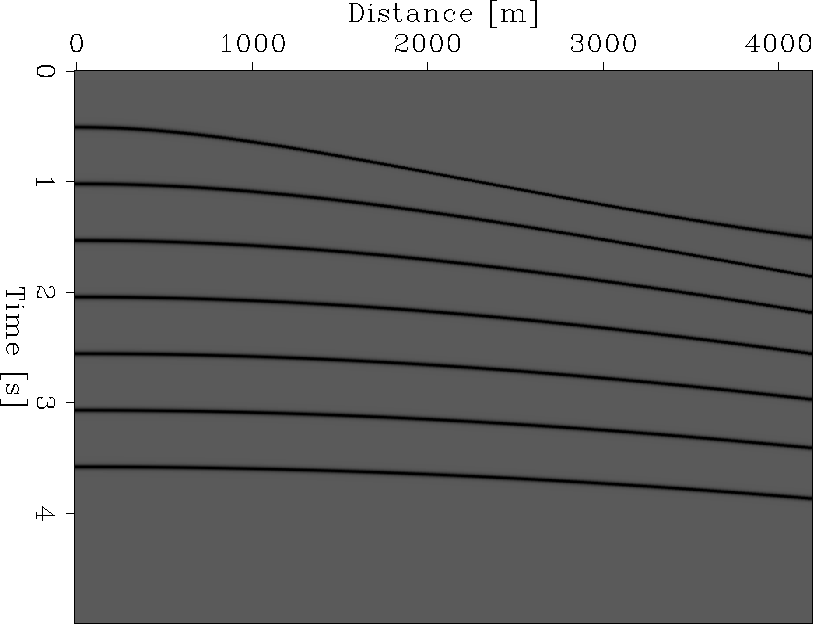
mod5NMO
Figure 2 Modeled data, using the non-hyperbolic equation with
a constant value of 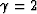 . . |
|  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





mod5NMO1
Figure 3 Modeled data, using the the traditional hyperbolic equation.
|
| 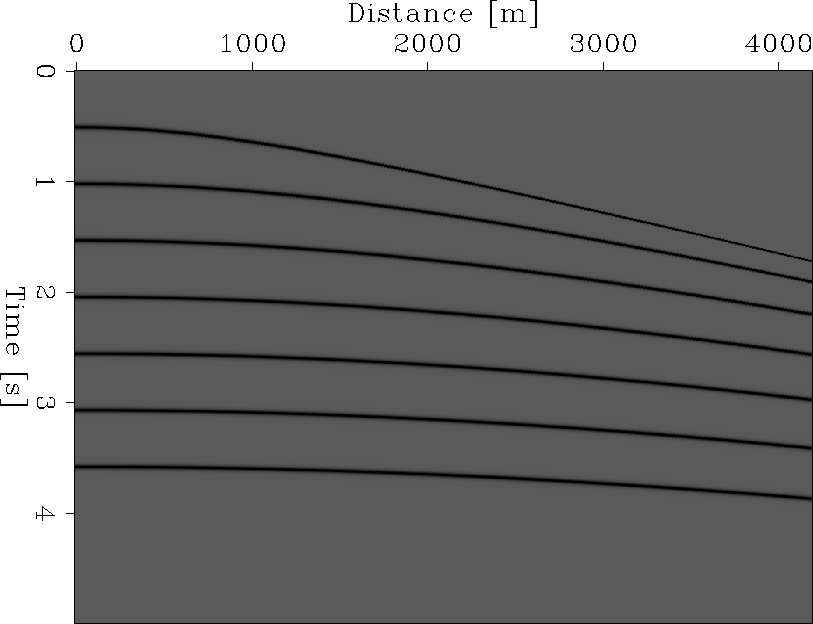 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





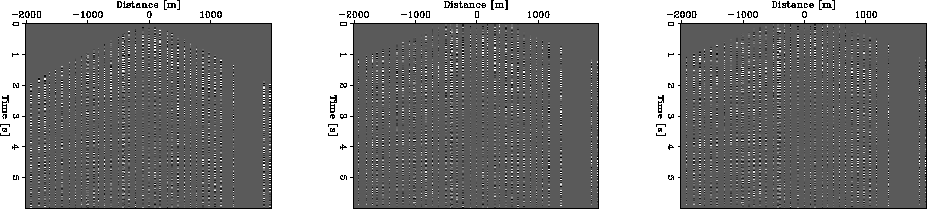
I also apply the non-hyperbolic moveout equation to a PS CMP gather from the Alba dataset
acquired
on the Alba oil field in the North sea. The data set is a multicomponent 3-D Ocean Bottom
Seismic experiment.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the original CMP gather before (left), after (center)
non-hyperbolic moveout, and after traditional hyperbolic moveout (right). I use
an initial velocity value of 1100 m/s, and a velocity gradient of 125
shows the original CMP gather before (left), after (center)
non-hyperbolic moveout, and after traditional hyperbolic moveout (right). I use
an initial velocity value of 1100 m/s, and a velocity gradient of 125 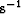 and
a constant
and
a constant 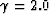 . Note that even though the events are not totally corrected, the non-hyperbolic
correction gives a better result for shallow events at large offsets. These events are flatter after
the non-hyperbolic moveout correction than with the hyperbolic moveout correction.
. Note that even though the events are not totally corrected, the non-hyperbolic
correction gives a better result for shallow events at large offsets. These events are flatter after
the non-hyperbolic moveout correction than with the hyperbolic moveout correction.
cmp_comp
Figure 4 PS CMP gather from the Alba dataset, original gather
(left), after non-hyperbolic moveout (center), and after traditional hyperbolic moveout (right).
I performed non-hyperbolic moveout and traditional moveout both with an initial velocity of 1100 m/s,
a velocity gradient of 125 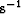 with
with 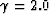 for the non-hyperbolic case.
for the non-hyperbolic case.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Conclusions and Future Work
Up: Rosales: NHNMO
Previous: Theory: Non-hyperbolic moveout
Stanford Exploration Project
10/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) present a hyperbolic moveout at
near offset or small offset-to-depth ratio. This result resembles the well known theoretical
presentation of
Tessmer and Behle (1988). However, the non-hyperbolic moveout is dominant for large offsets
and shallow depths, as
can be observed in Figure
) present a hyperbolic moveout at
near offset or small offset-to-depth ratio. This result resembles the well known theoretical
presentation of
Tessmer and Behle (1988). However, the non-hyperbolic moveout is dominant for large offsets
and shallow depths, as
can be observed in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.


![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)