




Next: Regularization of the LSJIMP
Up: The LSJIMP Inverse problem
Previous: LSJIMP: Least-squares minimization
The exact form of the modeling operators, 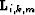 , shown in equation
(
, shown in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has not yet been discussed. Any candidate prestack
imaging operator for multiples must accomplish two tasks: focus the multiples in
time/depth and offset/angle at the position of the primary and correct their
amplitude to make the multiples directly comparable to the corresponding primary.
) has not yet been discussed. Any candidate prestack
imaging operator for multiples must accomplish two tasks: focus the multiples in
time/depth and offset/angle at the position of the primary and correct their
amplitude to make the multiples directly comparable to the corresponding primary.
The literature contains many multiple modeling techniques which use wavefield
extrapolation to ``add a multiple bounce'' to recorded data, and thus transform
primaries into a model of the multiples, which is then generally adaptively
subtracted from the data. These modeling techniques can roughly be divided into
earth-model-based
Berryhill and Kim (1986); Lu et al. (1999); Morley (1982); Wiggins (1988)
and autoconvolutional Riley and Claerbout (1976); Tsai (1985); Verschuur et al. (1992) approaches.
It is possible to reverse the multiple modeling process-in other words, to
``remove a multiple bounce'' from the data and transform multiples into
pseudo-primary events, which can then be imaged as primaries
Berkhout and Verschuur (2003); Shan (2003).
Existing migration techniques for multiples perform the reverse modeling process
either explicitly (i.e., using an earth model) or implicitly.
Reiter et al. (1991) imaged pegleg multiples with Kirchhoff prestack
depth migration. He and Schuster (2003) present a least-squares joint imaging
scheme for multiples that uses poststack Kirchhoff depth migration.
Yu and Schuster (2001) and Guitton (2002) migrate peglegs
with shot-profile depth migration, while Berkhout and Verschuur (1994) used a similar
crosscorrelation technique. Shan (2003) uses source-geophone migration after
crosscorrelation at the surface. None of these techniques explicitly addresses
the issue of amplitudes, beyond a polarity flip.
In this thesis, I use an earth-model-based multiple modeling strategy to simulate
the kinematics and angle-dependent amplitude behavior of pegleg multiples. In
section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I derive an extension to the normal moveout (NMO)
equation for pegleg multiples. In section
I derive an extension to the normal moveout (NMO)
equation for pegleg multiples. In section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I introduce HEMNO
(Heterogeneous Earth Multiple NMO Operator), an extension of the NMO equation for
multiples, which independently images split peglegs in a moderately heterogeneous
earth. In Sections
I introduce HEMNO
(Heterogeneous Earth Multiple NMO Operator), an extension of the NMO equation for
multiples, which independently images split peglegs in a moderately heterogeneous
earth. In Sections ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I derive a series
of amplitude correction operators to normalize the angle-dependent reflectivity
of imaged multiples to be commensurable with their imaged primaries.
I derive a series
of amplitude correction operators to normalize the angle-dependent reflectivity
of imaged multiples to be commensurable with their imaged primaries.
I postpone giving the full motivation for my particular choice of multiple
imaging operator, as well as many implementation details until section
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . However, we can at this early stage state some
important facts which have bearing on how the problem is regularized and how it
is implemented computationally. The prestack multiple image,
. However, we can at this early stage state some
important facts which have bearing on how the problem is regularized and how it
is implemented computationally. The prestack multiple image, 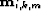 ,
shown in Figure
,
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , is parameterized by zero-offset
traveltime,
, is parameterized by zero-offset
traveltime,  , offset, x, and midpoint, y. However, one important
feature of the my combined imaging operator is the fact that it operates on a
CMP-by-CMP basis. This underscores the fact that HEMNO applies a vertical
stretch, and does not move information across midpoint. The regularization
schemes I present also do not operate across midpoint. This implementation
allows a coarse-grained parallelization scheme, enabling straightforward parallel
computation on a Linux cluster.
, offset, x, and midpoint, y. However, one important
feature of the my combined imaging operator is the fact that it operates on a
CMP-by-CMP basis. This underscores the fact that HEMNO applies a vertical
stretch, and does not move information across midpoint. The regularization
schemes I present also do not operate across midpoint. This implementation
allows a coarse-grained parallelization scheme, enabling straightforward parallel
computation on a Linux cluster.





Next: Regularization of the LSJIMP
Up: The LSJIMP Inverse problem
Previous: LSJIMP: Least-squares minimization
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I derive an extension to the normal moveout (NMO)
equation for pegleg multiples. In section
I derive an extension to the normal moveout (NMO)
equation for pegleg multiples. In section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I introduce HEMNO
(Heterogeneous Earth Multiple NMO Operator), an extension of the NMO equation for
multiples, which independently images split peglegs in a moderately heterogeneous
earth. In Sections
I introduce HEMNO
(Heterogeneous Earth Multiple NMO Operator), an extension of the NMO equation for
multiples, which independently images split peglegs in a moderately heterogeneous
earth. In Sections ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I derive a series
of amplitude correction operators to normalize the angle-dependent reflectivity
of imaged multiples to be commensurable with their imaged primaries.
I derive a series
of amplitude correction operators to normalize the angle-dependent reflectivity
of imaged multiples to be commensurable with their imaged primaries.