Next: HEMNO Implementation Issues
Up: Particular Implementation of LSJIMP
Previous: Estimation/Application of Seabed Reflection
HEMNO: Imaging of pegleg multiples in a heterogeneous earth
In Sections ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I developed a methodology,
valid in a laterally-homogenous earth, to image pegleg multiples and make their
amplitudes comparable to their primary. From Figure
I developed a methodology,
valid in a laterally-homogenous earth, to image pegleg multiples and make their
amplitudes comparable to their primary. From Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , recall that
a first-order pegleg consists of two unique arrivals: the event with a multiple
bounce over the source (``source-side'' pegleg), and the event with a bounce over
the receiver (``receiver-side'' pegleg). When reflectors dip, the arrivals have
different traveltimes on a CMP gather, and ``split'' into two separate events.
Figure
, recall that
a first-order pegleg consists of two unique arrivals: the event with a multiple
bounce over the source (``source-side'' pegleg), and the event with a bounce over
the receiver (``receiver-side'' pegleg). When reflectors dip, the arrivals have
different traveltimes on a CMP gather, and ``split'' into two separate events.
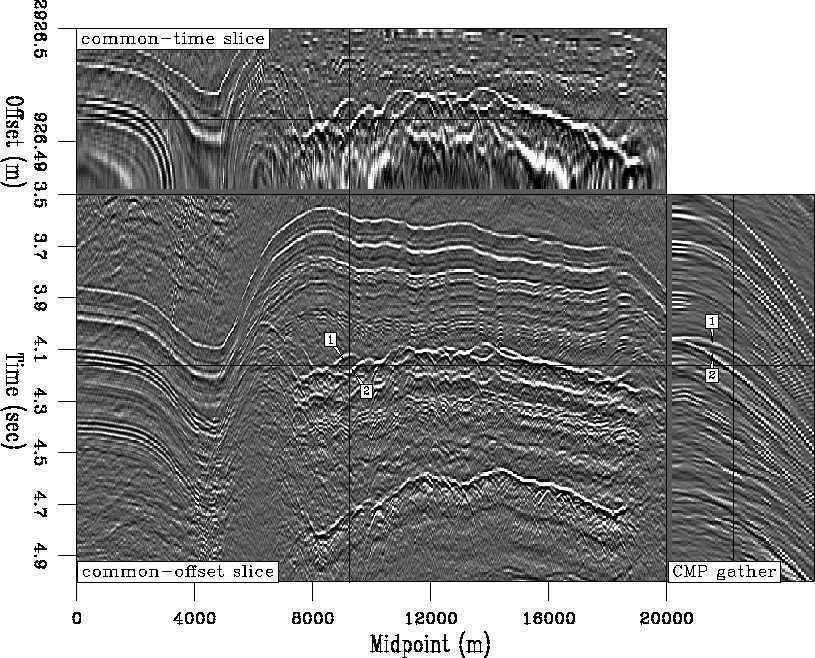
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the splitting phenomenon on the 2-D Gulf
of Mexico dataset which will be used extensively in Chapter
illustrates the splitting phenomenon on the 2-D Gulf
of Mexico dataset which will be used extensively in Chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The strong events in the ``crosshairs'' of the Figure
are the first-order source-side and receiver-side seabed pegleg multiples from
the top of salt reflection.
. The strong events in the ``crosshairs'' of the Figure
are the first-order source-side and receiver-side seabed pegleg multiples from
the top of salt reflection.
gulf.split
Figure 6 Splitting phenomenon observed on 2-D prestack
field data from the Gulf of Mexico (used in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The seabed pegleg from the top of salt reflection splits noticeably into two
distinct events (labels ``1'' and ``2''). On the CMP gather the apexes of the
two legs are shifted away from zero offset.
).
The seabed pegleg from the top of salt reflection splits noticeably into two
distinct events (labels ``1'' and ``2''). On the CMP gather the apexes of the
two legs are shifted away from zero offset.





On CMP gathers, primary reflection hyperbolas generally have apexes at zero
offset. Levin and Shah (1977) show that the apexes of split pegleg
multiples shift away from zero offset, raising the apparent velocity of one leg
(on one-sided marine data), which can hamper velocity analysis and Radon multiple
suppression. Hargreaves et al. (2003) use an apex-shifted Radon transform for
demultiple.
Even if reflectors dip only mildly, a prestack imaging method for peglegs must
account for splitting. Mild variations in reflector depth over a cable length
can introduce considerable destructive interference between the legs of a pegleg
multiple at far offsets. This interference, is impossible to model with a 1-D
theory, introduces false amplitude-versus-offset (AVO) behavior in the multiples,
and certainly would hamper any attempts to use multiples as a constraint on the
AVO signature of the primaries Levin (1996).
Levin and Shah (1977) deduced analytic kinematic moveout equations for
split 2-D pegleg multiples, and Ross et al. (1999) extended the work to
3-D. Both approaches assume constant velocity and locally planar reflectors -
depending on local geology, this may be unrealistic in practice. In this thesis,
my particular implementation of LSJIMP relies on a simplified moveout equation
based upon a more practically realizable conceptual model, which I call HEMNO
(Heterogeneous Earth Multiple NMO Operator). In Appendix
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I prove that for small reflector dips, the HEMNO
traveltime equation reduces to Levin and Shah's moveout equations.
I prove that for small reflector dips, the HEMNO
traveltime equation reduces to Levin and Shah's moveout equations.
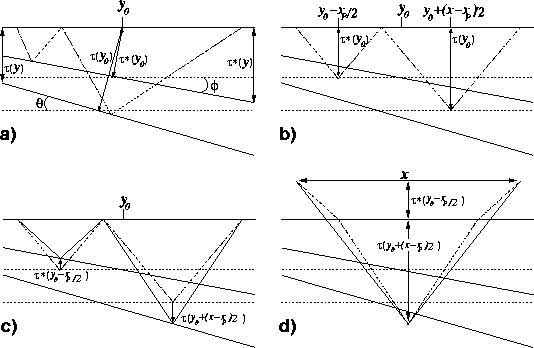
schem-pegleg-dip2
Figure 7 HEMNO operator schematic. (a) True
raypath in constant-velocity earth. The zero-offset traveltimes to the seabed
and subsea reflector are 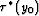 and
and 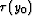 , respectively. (b)
Assumed reflection points under flat-earth assumption. xp is defined in
equation (
, respectively. (b)
Assumed reflection points under flat-earth assumption. xp is defined in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). (c) Stretch legs of raypath vertically to
match measured
). (c) Stretch legs of raypath vertically to
match measured 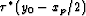 and
and 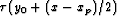 . Panel (d)
Connect legs of raypath. The solid line that connects the reassembled raypath
is the final result.
. Panel (d)
Connect legs of raypath. The solid line that connects the reassembled raypath
is the final result.

Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) graphically illustrates the HEMNO derivation
in a constant-velocity earth. Panel a) illustrates the raypath of the ``S102G''
pegleg where the multiple generator and target reflector dip. Panel b)
illustrates the raypath implied by the 1-D multiple imaging theory derived in
Section
graphically illustrates the HEMNO derivation
in a constant-velocity earth. Panel a) illustrates the raypath of the ``S102G''
pegleg where the multiple generator and target reflector dip. Panel b)
illustrates the raypath implied by the 1-D multiple imaging theory derived in
Section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) : the primary leg of the multiple has offset
xp [equation (
: the primary leg of the multiple has offset
xp [equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )] and the zero-offset traveltime to both
reflectors is spatially invariant. Panel c) illustrates the HEMNO strategy: we
account for spatially-variant reflector geometry by vertically stretching the
1-D raypath to match the zero-offset traveltime at the reflection points.
However, the solid raypath in panel c) disobeys Snell's Law, so to obtain the
final result in panel d), the tails of the legs of the ray are simply connected
to produce a valid raypath, which has the equation of a hyperbola with offset
x and zero-offset traveltime
)] and the zero-offset traveltime to both
reflectors is spatially invariant. Panel c) illustrates the HEMNO strategy: we
account for spatially-variant reflector geometry by vertically stretching the
1-D raypath to match the zero-offset traveltime at the reflection points.
However, the solid raypath in panel c) disobeys Snell's Law, so to obtain the
final result in panel d), the tails of the legs of the ray are simply connected
to produce a valid raypath, which has the equation of a hyperbola with offset
x and zero-offset traveltime 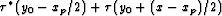 . We
first define for simplicity
. We
first define for simplicity
| 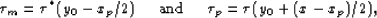 |
(26) |
and then write the HEMNO equation:
| 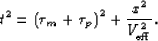 |
(27) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) flattens one leg of a first-order pegleg in offset and
shifts the event to the zero-offset traveltime of the primary. By using
) flattens one leg of a first-order pegleg in offset and
shifts the event to the zero-offset traveltime of the primary. By using
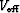 , we ignore lateral velocity variations, which is consistent with
the assumption of small dips. Similar expressions may be derived for other
multiple events, but I omit the derivations for brevity. Figure
, we ignore lateral velocity variations, which is consistent with
the assumption of small dips. Similar expressions may be derived for other
multiple events, but I omit the derivations for brevity. Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates application of the HEMNO equation to the
split top of salt pegleg shown in Figure
illustrates application of the HEMNO equation to the
split top of salt pegleg shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
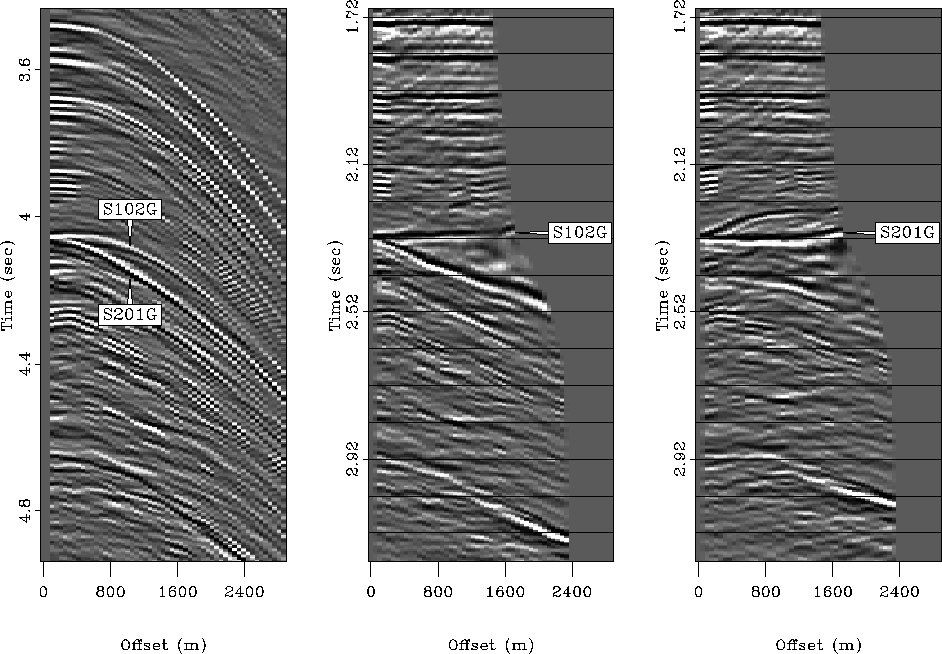
gulf.hemno.split
Figure 8 Left: CMP gather extracted from midpoint
9200 m of the Mississippi Canyon data cube shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice the split top of salt pegleg at
. Notice the split top of salt pegleg at  . Center and Right: HEMNO equation applied to two splits. Notice how the events
are independently focused in time and offset. The images panels have also
undergone normalized Snell Resampling, differential geometric spreading
correction, and application of the seabed reflection coefficient.
. Center and Right: HEMNO equation applied to two splits. Notice how the events
are independently focused in time and offset. The images panels have also
undergone normalized Snell Resampling, differential geometric spreading
correction, and application of the seabed reflection coefficient.










Next: HEMNO Implementation Issues
Up: Particular Implementation of LSJIMP
Previous: Estimation/Application of Seabed Reflection
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I developed a methodology,
valid in a laterally-homogenous earth, to image pegleg multiples and make their
amplitudes comparable to their primary. From Figure
I developed a methodology,
valid in a laterally-homogenous earth, to image pegleg multiples and make their
amplitudes comparable to their primary. From Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , recall that
a first-order pegleg consists of two unique arrivals: the event with a multiple
bounce over the source (``source-side'' pegleg), and the event with a bounce over
the receiver (``receiver-side'' pegleg). When reflectors dip, the arrivals have
different traveltimes on a CMP gather, and ``split'' into two separate events.
Figure
, recall that
a first-order pegleg consists of two unique arrivals: the event with a multiple
bounce over the source (``source-side'' pegleg), and the event with a bounce over
the receiver (``receiver-side'' pegleg). When reflectors dip, the arrivals have
different traveltimes on a CMP gather, and ``split'' into two separate events.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the splitting phenomenon on the 2-D Gulf
of Mexico dataset which will be used extensively in Chapter
illustrates the splitting phenomenon on the 2-D Gulf
of Mexico dataset which will be used extensively in Chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The strong events in the ``crosshairs'' of the Figure
are the first-order source-side and receiver-side seabed pegleg multiples from
the top of salt reflection.
. The strong events in the ``crosshairs'' of the Figure
are the first-order source-side and receiver-side seabed pegleg multiples from
the top of salt reflection.