




Next: Amplitude corrections for pegleg
Up: Particular Implementation of LSJIMP
Previous: Particular Implementation of LSJIMP
Kinematic imaging of pegleg multiples in a laterally-homogeneous earth
In a ``1-D Earth'' (horizontally-stratified, v(z) medium), the normal-moveout
(NMO) equation Taner and Koehler (1969) describes the prestack traveltime curve
of a primary reflection at relatively short source-receiver offset:
| 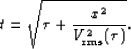 |
(16) |
Applied as an offset-dependent vertical time shift to a CMP gather, the NMO
equation flattens an arbitrary primary to its zero-offset traveltime  ,
where (half) offset is denoted x and the root-mean-square (RMS) velocity,
,
where (half) offset is denoted x and the root-mean-square (RMS) velocity,
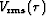 , is defined in a laterally-homogeneous earth as:
, is defined in a laterally-homogeneous earth as:
| 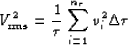 |
(17) |
The earth is parameterized by 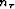 layers of time thickness
layers of time thickness 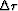 ,
with constant interval velocity vi in each layer.
,
with constant interval velocity vi in each layer.
Analogously, a modified NMO equation can image pegleg multiples in a 1-D Earth,
as motivated graphically by Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . From the figure, we see that
kinematically, a first-order pegleg can be conceptualized as a ``pseudo-primary''
with the same offset, but with an additional two-way zero-offset traveltime to
the multiple generator,
. From the figure, we see that
kinematically, a first-order pegleg can be conceptualized as a ``pseudo-primary''
with the same offset, but with an additional two-way zero-offset traveltime to
the multiple generator, 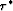 . In equation form, let us extend this intuition
to the general case of a
. In equation form, let us extend this intuition
to the general case of a 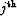 -order pegleg to write an NMO equation for
peglegs:
-order pegleg to write an NMO equation for
peglegs:
| 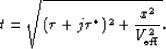 |
(18) |
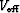 is the effective RMS velocity of the pseudo-primary shown in Figure
is the effective RMS velocity of the pseudo-primary shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . To derive an expression for
. To derive an expression for 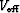 , we modify the
definition of RMS velocity, equation (
, we modify the
definition of RMS velocity, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), to reflect a
), to reflect a
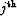 -order pegleg multiple's additional travel between the surface and
multiple generator:
-order pegleg multiple's additional travel between the surface and
multiple generator:
| 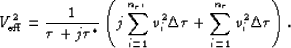 |
(19) |
Analogously, 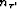 is the number of assumed layers between the earth's
surface and the multiple generator. Notice that the two terms inside the
parentheses of equation (
is the number of assumed layers between the earth's
surface and the multiple generator. Notice that the two terms inside the
parentheses of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are simply the definition of RMS
velocity at
) are simply the definition of RMS
velocity at 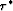 and
and  , respectively. We can substitute equation
(
, respectively. We can substitute equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) accordingly to derive the final expression for
) accordingly to derive the final expression for 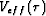 :
:
| 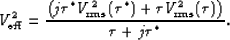 |
(20) |
Wang (2003) derives a similar series of expressions.
schem
Figure 3 Pegleg multiples ``S201G'' and ``S102G'' have the
same traveltimes as ``pseudo-primary'' with the same offset and an extra
zero-offset traveltime 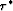 . . |
|  |






Next: Amplitude corrections for pegleg
Up: Particular Implementation of LSJIMP
Previous: Particular Implementation of LSJIMP
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . From the figure, we see that
kinematically, a first-order pegleg can be conceptualized as a ``pseudo-primary''
with the same offset, but with an additional two-way zero-offset traveltime to
the multiple generator,
. From the figure, we see that
kinematically, a first-order pegleg can be conceptualized as a ``pseudo-primary''
with the same offset, but with an additional two-way zero-offset traveltime to
the multiple generator, ![]() . In equation form, let us extend this intuition
to the general case of a
. In equation form, let us extend this intuition
to the general case of a ![]() -order pegleg to write an NMO equation for
peglegs:
-order pegleg to write an NMO equation for
peglegs:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . To derive an expression for
. To derive an expression for ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), to reflect a
), to reflect a
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are simply the definition of RMS
velocity at
) are simply the definition of RMS
velocity at ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) accordingly to derive the final expression for
) accordingly to derive the final expression for 