Next: Playing Devil's Advocate: What
Up: 2-D Field Data Results
Previous: A closer look at
Verschuur et al. (1992) of Delft University presented a very effective
autoconvolutional modeling technique for surface-related multiples, known as the
``SRME'' (Surface-related Multiple Elimination) method. Assuming sufficiently
dense source coverage, as is typical with 2-D towed-streamer marine data, the
method accurately models all multiples which bounce downward at the acquisition
datum, but nowhere else. SRME can model diffracted multiples and other complex
events, and most compellingly, requires no prior knowledge of the subsurface
geology. Once estimated, the SRME multiple model is usually subtracted from the
recorded data by any number of adaptive subtraction techniques.
Postponing a discussion of SRME's limitations with 3-D narrow azimuth marine
data until Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the method has a number of
limitations in 2-D. The method obtains a multiple model by iteratively adding
terms of an infinite series, although in practice only one iteration is done.
After one iteration, the wavelet of the multiple model will generally be
stretched somewhat because it is generated via autoconvolution. Additionally,
the near-offset gap of the multiple model is twice that in the data. Since
near-offset multiple energy contributes most to the stack, accurate
extrapolation of the near-offset traces is crucial. Another limitation of SRME
is its tendency to ``over-predict'' higher-order multiples; this may hamper some
subtraction algorithms.
, the method has a number of
limitations in 2-D. The method obtains a multiple model by iteratively adding
terms of an infinite series, although in practice only one iteration is done.
After one iteration, the wavelet of the multiple model will generally be
stretched somewhat because it is generated via autoconvolution. Additionally,
the near-offset gap of the multiple model is twice that in the data. Since
near-offset multiple energy contributes most to the stack, accurate
extrapolation of the near-offset traces is crucial. Another limitation of SRME
is its tendency to ``over-predict'' higher-order multiples; this may hamper some
subtraction algorithms.
In this section, I compare an SRME multiple model (one iteration), computed by
Antoine Guitton, with a multiple model generated by the method outlined
previously for the computation of crosstalk (section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
using HEMNO as the imaging engine. Figures
),
using HEMNO as the imaging engine. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare the SRME and HEMNO results at CMP locations 55
(1440 m) and 344 (9150 m), respectively. The results of LSJIMP at same CMP
locations are shown in Figures
compare the SRME and HEMNO results at CMP locations 55
(1440 m) and 344 (9150 m), respectively. The results of LSJIMP at same CMP
locations are shown in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
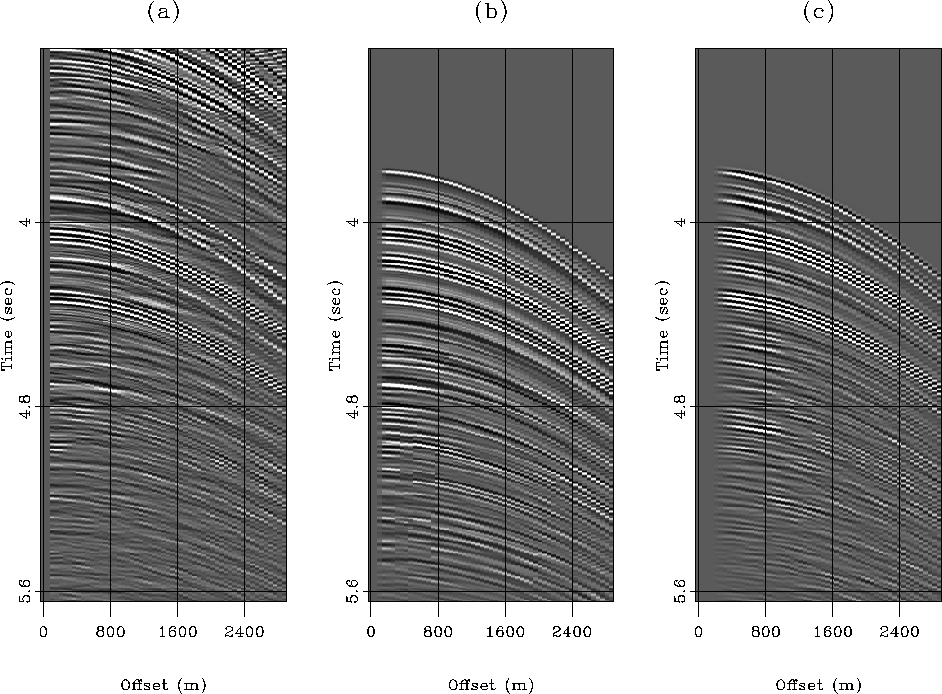
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is taken from the sedimentary basin portion of
the Mississippi Canyon data. We first notice the improved near-offset coverage
of the HEMNO model. Kinematically, both HEMNO and SRME match the shallow
multiple events quite accurately. Deeper in the gather, we see little order to
the multiples in the data. Many of the primaries in the 2.5-3.5 second range
may come from out-of-plane reflectors or diffractors, hence the multiples of
these events will not have the expected kinematics. In 2-D, both HEMNO and SRME
assume that all energy propagates in the plane of acquisition. Figure
is taken from the sedimentary basin portion of
the Mississippi Canyon data. We first notice the improved near-offset coverage
of the HEMNO model. Kinematically, both HEMNO and SRME match the shallow
multiple events quite accurately. Deeper in the gather, we see little order to
the multiples in the data. Many of the primaries in the 2.5-3.5 second range
may come from out-of-plane reflectors or diffractors, hence the multiples of
these events will not have the expected kinematics. In 2-D, both HEMNO and SRME
assume that all energy propagates in the plane of acquisition. Figure
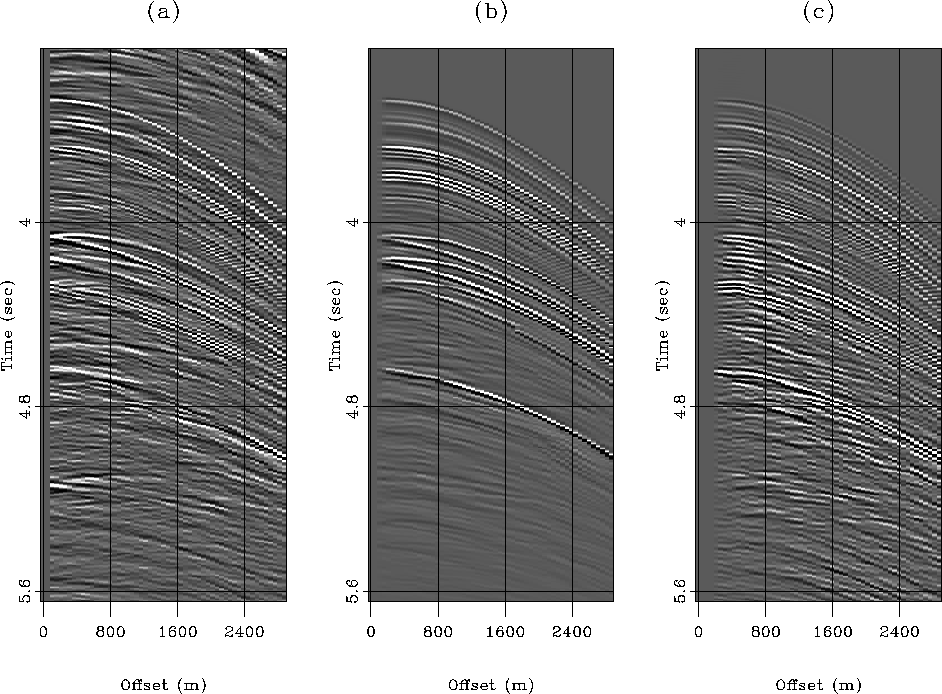
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is taken from over the salt body. Notice that both
the HEMNO and SRME models fairly accurately represent the strong split peglegs
from the top of salt reflection.
is taken from over the salt body. Notice that both
the HEMNO and SRME models fairly accurately represent the strong split peglegs
from the top of salt reflection.
delft.comp.55
Figure 21 HEMNO versus SRME comparison, CMP 55
(1440m). Left: raw data. Center: HEMNO multiple model. Right: SRME
multiple model.





delft.comp.344
Figure 22 HEMNO versus SRME comparison, CMP 344
(9150). Left: raw data. Center: HEMNO multiple model. Right: SRME
multiple model.





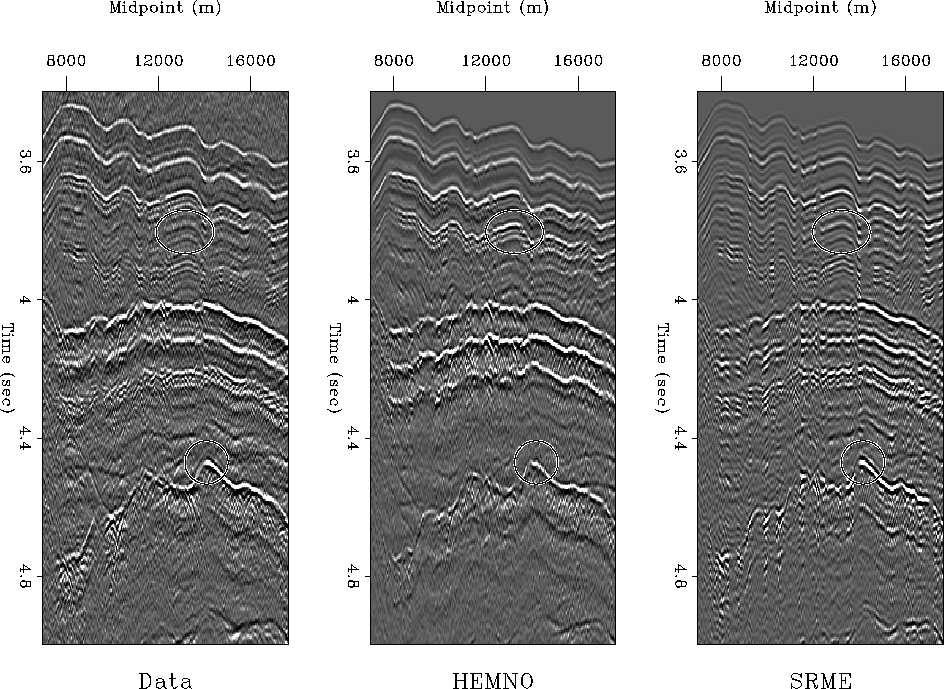
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare the HEMNO
and SRME multiple models on constant-offset sections. Here, we can check each
model for correct event positioning-especially important when complex peglegs
split. On a near-offset section (Figure
compare the HEMNO
and SRME multiple models on constant-offset sections. Here, we can check each
model for correct event positioning-especially important when complex peglegs
split. On a near-offset section (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we see that
both methods accurately match the kinematics of the important multiple
reflections. The region highlighted by the circle illustrates the stretched
wavelet of the SRME model. The region highlighted by the oval shows how the
poorly-estimated R1 reflection coefficient has caused an overly strong event to
appear in the HEMNO model. On a medium-offset section
(Figure
), we see that
both methods accurately match the kinematics of the important multiple
reflections. The region highlighted by the circle illustrates the stretched
wavelet of the SRME model. The region highlighted by the oval shows how the
poorly-estimated R1 reflection coefficient has caused an overly strong event to
appear in the HEMNO model. On a medium-offset section
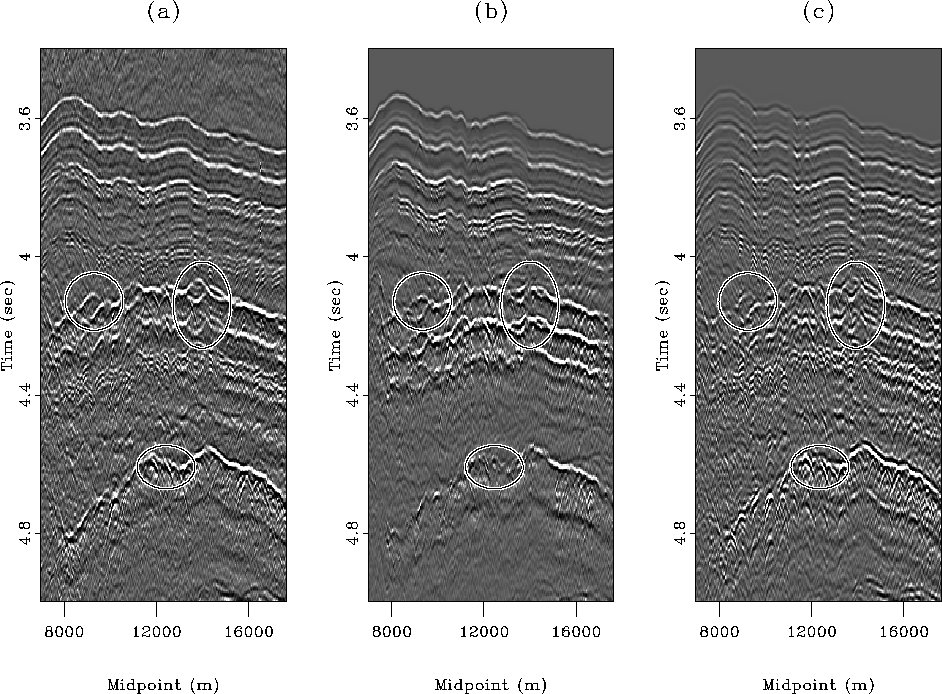
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we again see that both models roughly mimic
the multiples in the data. Of special interest is the positioning of split
multiple events. In the region highlighted by the circle, all three methods
correctly model the split pegleg. The amplitudes on the HEMNO model appear
truer to the data. In the region highlighted by the tall oval, we see that the
HEMNO model does not accurately represent the data, but the SRME model does. In
the region highlighted by the wide oval, we see that SRME better models the
diffractions and other features of the complex top of salt pure multiple.
) we again see that both models roughly mimic
the multiples in the data. Of special interest is the positioning of split
multiple events. In the region highlighted by the circle, all three methods
correctly model the split pegleg. The amplitudes on the HEMNO model appear
truer to the data. In the region highlighted by the tall oval, we see that the
HEMNO model does not accurately represent the data, but the SRME model does. In
the region highlighted by the wide oval, we see that SRME better models the
diffractions and other features of the complex top of salt pure multiple.
delft.noffcomp
Figure 23 HEMNO versus SRME near-offset comparison.
Left: raw data. Center: HEMNO multiple model. Right: SRME multiple model.
Regions of interest are highlighted.





delft.moffcomp
Figure 24 HEMNO versus SRME medium-offset comparison.
Left: raw data. Center: HEMNO multiple model. Right: SRME multiple model.
Regions of interest are highlighted.










Next: Playing Devil's Advocate: What
Up: 2-D Field Data Results
Previous: A closer look at
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the method has a number of
limitations in 2-D. The method obtains a multiple model by iteratively adding
terms of an infinite series, although in practice only one iteration is done.
After one iteration, the wavelet of the multiple model will generally be
stretched somewhat because it is generated via autoconvolution. Additionally,
the near-offset gap of the multiple model is twice that in the data. Since
near-offset multiple energy contributes most to the stack, accurate
extrapolation of the near-offset traces is crucial. Another limitation of SRME
is its tendency to ``over-predict'' higher-order multiples; this may hamper some
subtraction algorithms.
, the method has a number of
limitations in 2-D. The method obtains a multiple model by iteratively adding
terms of an infinite series, although in practice only one iteration is done.
After one iteration, the wavelet of the multiple model will generally be
stretched somewhat because it is generated via autoconvolution. Additionally,
the near-offset gap of the multiple model is twice that in the data. Since
near-offset multiple energy contributes most to the stack, accurate
extrapolation of the near-offset traces is crucial. Another limitation of SRME
is its tendency to ``over-predict'' higher-order multiples; this may hamper some
subtraction algorithms.