Next: Combined LSJIMP Data and
Up: The LSJIMP Inverse problem
Previous: Regularization 2: Differencing across
The third and final discriminant between crosstalk and signal exploits the
inherent predictability of the crosstalk to suppress it. If we have an estimate
of the signal, we can directly model the expected crosstalk events on each
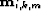 , and construct a model-space weighting function to penalize
crosstalk. Unfortunately, unless we employ a nonlinear iteration (see section
, and construct a model-space weighting function to penalize
crosstalk. Unfortunately, unless we employ a nonlinear iteration (see section
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we do not, a priori, have this signal estimate.
However, between the seabed reflection and the onset of its first multiple, the
recorded data contains only primaries (inter-bed multiples and locally-converted
shear waves are generally weak), and it is these strong, shallow events that
often spawn the most troublesome crosstalk events. Therefore, we can directly
model any pegleg multiple arising from a multiple generator with traveltime less
than that of the first seabed multiple.
), we do not, a priori, have this signal estimate.
However, between the seabed reflection and the onset of its first multiple, the
recorded data contains only primaries (inter-bed multiples and locally-converted
shear waves are generally weak), and it is these strong, shallow events that
often spawn the most troublesome crosstalk events. Therefore, we can directly
model any pegleg multiple arising from a multiple generator with traveltime less
than that of the first seabed multiple.
If we define 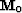 as an operator that applies a flat mute below twice the
zero-offset traveltime of the seabed, and
as an operator that applies a flat mute below twice the
zero-offset traveltime of the seabed, and 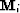 as a similar operator that
mutes above the zero-offset traveltime of the
as a similar operator that
mutes above the zero-offset traveltime of the 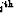 multiple generator,
then
multiple generator,
then
| 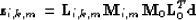 |
(9) |
is a model of the 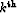 leg of the
leg of the 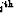 order multiple from the
order multiple from the
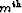 multiple generator. Each
multiple generator. Each 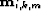 in equation
(
in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) should ideally contain only the
) should ideally contain only the 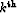 leg of the
leg of the
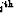 -order multiple from the
-order multiple from the 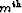 multiple generator - all other
energy is crosstalk. To simulate crosstalk noise in
multiple generator - all other
energy is crosstalk. To simulate crosstalk noise in 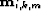 , we apply
, we apply
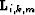 to all multiple model panels
to all multiple model panels  (except
(except
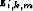 ) and sum:
) and sum:
| 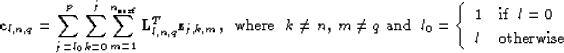 |
(10) |
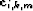 is a kinematic model of crosstalk for
is a kinematic model of crosstalk for 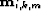 . It
could be used as a traditional multiple model (see section
. It
could be used as a traditional multiple model (see section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and subtracted from the data, but I instead convert each
)
and subtracted from the data, but I instead convert each 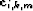 into a
weighting function by taking the absolute value. We can write the model residual
corresponding to the third model regularization operator:
into a
weighting function by taking the absolute value. We can write the model residual
corresponding to the third model regularization operator:
| ![\begin{displaymath}
\bold r_m^{[3]}[i,k,m](\tau,x) = \left\vert \bold c_{i,k,m}(\tau,x) \right\vert \; \bold m_{i,k,m}(\tau,x).\end{displaymath}](img44.gif) |
(11) |
Although the crosstalk weights will likely overlap (and damage) signal to some
extent, the signal's flatness and self-consistency between images ensures that
regularization operators (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will
``spread'' redundant information about the primaries from other
) will
``spread'' redundant information about the primaries from other 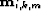 and other offsets to compensate for any losses. Figure
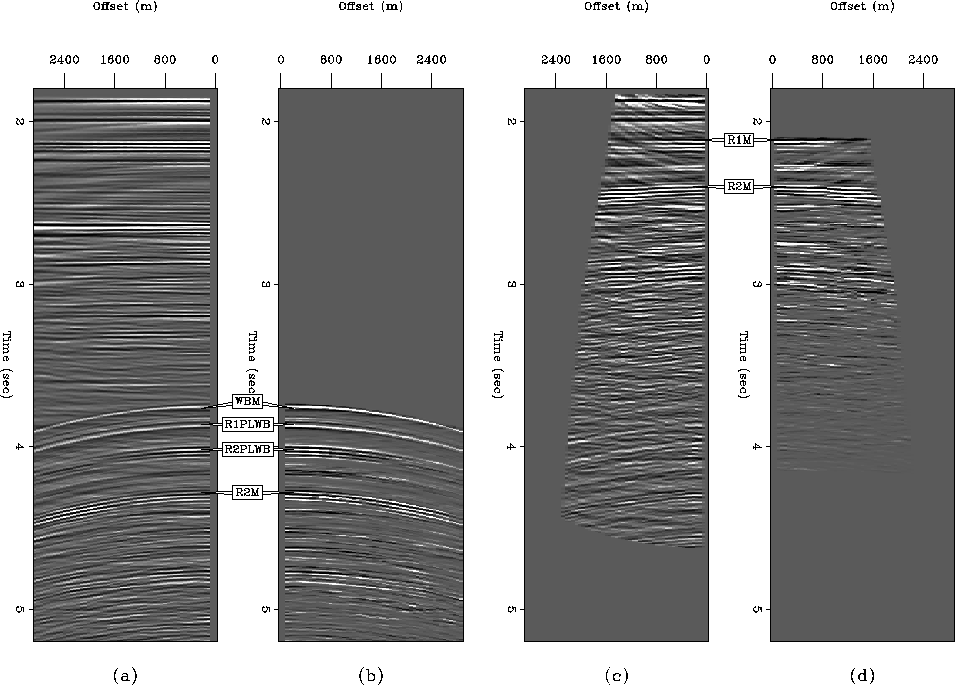
and other offsets to compensate for any losses. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the application of the crosstalk weights for the primary image and a
multiple image. On panel (a), the primary image, the crosstalk is the obviously
curving events. On panel (c), the seabed pegleg image, the crosstalk events are
multiples from other multiple generators (e.g., R1M and R2M). Notice that in
both cases the unwanted multiples are picked cleanly out of the data, leaving
the underlying signal intact.
crosstalk.gulf
illustrates the application of the crosstalk weights for the primary image and a
multiple image. On panel (a), the primary image, the crosstalk is the obviously
curving events. On panel (c), the seabed pegleg image, the crosstalk events are
multiples from other multiple generators (e.g., R1M and R2M). Notice that in
both cases the unwanted multiples are picked cleanly out of the data, leaving
the underlying signal intact.
crosstalk.gulf
Figure 2 Application of crosstalk weights to real CMP
after prestack imaging. Panel (a): primary image, 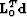 . Panel (b): weighted primary image,
. Panel (b): weighted primary image, 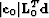 . Panel
(c): seabed pegleg image,
. Panel
(c): seabed pegleg image, 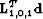 . Panel (d): weighted
seabed pegleg image,
. Panel (d): weighted
seabed pegleg image, 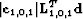 .
.
 in this case. Prominent crosstalk events are labeled on the
various panels.
in this case. Prominent crosstalk events are labeled on the
various panels.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Combined LSJIMP Data and
Up: The LSJIMP Inverse problem
Previous: Regularization 2: Differencing across
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we do not, a priori, have this signal estimate.
However, between the seabed reflection and the onset of its first multiple, the
recorded data contains only primaries (inter-bed multiples and locally-converted
shear waves are generally weak), and it is these strong, shallow events that
often spawn the most troublesome crosstalk events. Therefore, we can directly
model any pegleg multiple arising from a multiple generator with traveltime less
than that of the first seabed multiple.
), we do not, a priori, have this signal estimate.
However, between the seabed reflection and the onset of its first multiple, the
recorded data contains only primaries (inter-bed multiples and locally-converted
shear waves are generally weak), and it is these strong, shallow events that
often spawn the most troublesome crosstalk events. Therefore, we can directly
model any pegleg multiple arising from a multiple generator with traveltime less
than that of the first seabed multiple.
![]() as an operator that applies a flat mute below twice the
zero-offset traveltime of the seabed, and
as an operator that applies a flat mute below twice the
zero-offset traveltime of the seabed, and ![]() as a similar operator that
mutes above the zero-offset traveltime of the
as a similar operator that
mutes above the zero-offset traveltime of the ![]() multiple generator,
then
multiple generator,
then
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) should ideally contain only the
) should ideally contain only the 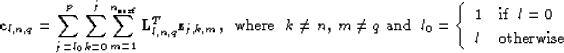
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and subtracted from the data, but I instead convert each
)
and subtracted from the data, but I instead convert each ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will
``spread'' redundant information about the primaries from other
) will
``spread'' redundant information about the primaries from other ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the application of the crosstalk weights for the primary image and a
multiple image. On panel (a), the primary image, the crosstalk is the obviously
curving events. On panel (c), the seabed pegleg image, the crosstalk events are
multiples from other multiple generators (e.g., R1M and R2M). Notice that in
both cases the unwanted multiples are picked cleanly out of the data, leaving
the underlying signal intact.
illustrates the application of the crosstalk weights for the primary image and a
multiple image. On panel (a), the primary image, the crosstalk is the obviously
curving events. On panel (c), the seabed pegleg image, the crosstalk events are
multiples from other multiple generators (e.g., R1M and R2M). Notice that in
both cases the unwanted multiples are picked cleanly out of the data, leaving
the underlying signal intact.