Biondi and Tisserant (2004) extend the 2-D RMO function
(equation (1)) to a 3-D function that includes the
azimuth of the reflector (![]() ), and the azimuth of the
reflection (
), and the azimuth of the
reflection (![]() ):
):
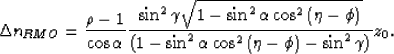 |
(3) |
Figure 5 synthesizes all the
velocity analysis done with equation (3) on two
CIGs taken from the model.
CIG700 (top) and CIG425 (bottom) stacked over
![]() are represented in Figure 5a.
are represented in Figure 5a.
|
stk_3D_700_450
Figure 5 Velocity error analysis by semblance using a 3-D RMO function on CIG700 on the top row, and on CIG425 on the bottom row. a) CIG after stack over |  |
Figure 5b is the semblance
analysis of the stack using the 3-D RMO function (equation
(3)),
with ![]() (the true azimuth of the reflectors) and
assuming
(the true azimuth of the reflectors) and
assuming ![]() in the absence of
in the absence of ![]() information.
For the first CIG, the comparison with the
semblance panel obtained with the 2-D RMO function
(Figure 4c) shows a more
accurate resolution of the velocity error when the reflector
azimuth is provided.
information.
For the first CIG, the comparison with the
semblance panel obtained with the 2-D RMO function
(Figure 4c) shows a more
accurate resolution of the velocity error when the reflector
azimuth is provided.
|
pfan_700_450
Figure 6 Reflection azimuth analysis using a 3-D RMO function on a) CIG700 b) CIG425. All semblance panels are squared to increase resolution. |  |
We perform a semblance analysis to determine the reflection azimuth.
The procedure consists in scanning all the slices at
constant ![]() of the
(z,
of the
(z,![]() ,
,![]() ) cube using equation (3), with
the velocity error obtained from a previous analysis performed
on the stack with the
) cube using equation (3), with
the velocity error obtained from a previous analysis performed
on the stack with the ![]() assumption (Figure
5b).
Then, only the trace corresponding to the measured velocity
error is
taken from each semblance panel at constant
assumption (Figure
5b).
Then, only the trace corresponding to the measured velocity
error is
taken from each semblance panel at constant ![]() .
All the traces displayed side by side form the
.
All the traces displayed side by side form the ![]() semblance panel
displayed in Figure 6. The peaks
of semblance give the reflection azimuth for each event.
The value of
semblance panel
displayed in Figure 6. The peaks
of semblance give the reflection azimuth for each event.
The value of ![]() ranges from
ranges from ![]() to
to ![]() for the first CIG, and from
for the first CIG, and from
![]() to
to ![]() for the second CIG.
They are consistent with the
for the second CIG.
They are consistent with the ![]() values read on
Figure 3.
Once again, the reflection azimuths are comparable at
similar reflector dips.
values read on
Figure 3.
Once again, the reflection azimuths are comparable at
similar reflector dips.
Figure 5c adds the reflection azimuth
information picked in Figure 6 to the velocity
error analysis. This extra information
does not improve the resolution of the velocity error for
the first CIG, where the range of ![]() is limited and
satisfies the
is limited and
satisfies the ![]() assumption because of the limited dips.
Note that the peaks of semblance are not centered perfectly
on
assumption because of the limited dips.
Note that the peaks of semblance are not centered perfectly
on ![]() but are closer to
but are closer to ![]() . This underestimated
velocity error is due to the straight rays assumption
that over-corrects the move-out.
. This underestimated
velocity error is due to the straight rays assumption
that over-corrects the move-out.
For the second CIG, where the ![]() assumption is not
valid,
we expect some changes. Paradoxically, the estimation seems less
accurate for the
assumption is not
valid,
we expect some changes. Paradoxically, the estimation seems less
accurate for the ![]() reflector when the value of
reflector when the value of ![]() is used (
is used (![]() ) instead of setting
) instead of setting ![]() to
(
to
(![]() ).
The reason is when the
).
The reason is when the ![]() approximation is not valid,
the RMO function over-estimates the velocity error.
Simultaneously, the RMO function under-estimates the
velocity error because of the straight rays approximation.
Hence the errors cancel out and make the estimation
apparently more accurate with the
approximation is not valid,
the RMO function over-estimates the velocity error.
Simultaneously, the RMO function under-estimates the
velocity error because of the straight rays approximation.
Hence the errors cancel out and make the estimation
apparently more accurate with the ![]() assumption
than with the correct value of
assumption
than with the correct value of ![]() .
.
The 3-D analysis of the RMO in the ADCIGs improves the resolution of the velocity error, even if the knowledge of the reflection azimuth does not bring visible improvement. The precise estimation of the reflection azimuth still holds for tomographic or amplitude-versus-angle studies.