ABSTRACT
A general analysis of poroelasticity for vertical transverse isotropy (VTI)
shows that four eigenvectors are pure shear modes with no coupling to
the pore-fluid mechanics. The remaining two eigenvectors are linear
combinations of pure compression and uniaxial shear, both of which are
coupled to the fluid mechanics. After reducing the problem to a 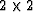 system, the analysis shows in a relatively elementary fashion how a
poroelastic system with isotropic solid elastic frame but with
anisotropy introduced through the poroelastic coefficients interacts
with the mechanics of the pore fluid and produces shear dependence
on fluid properties in the overall poroelastic system. The analysis
shows, for example, that this effect is always present (though sometimes
small in magnitude) in the systems studied, and can be quite large
(up to a definite maximum increase of 20 per cent)
in some rocks - including Spirit River sandstone and
Schuler-Cotton Valley sandstone. system, the analysis shows in a relatively elementary fashion how a
poroelastic system with isotropic solid elastic frame but with
anisotropy introduced through the poroelastic coefficients interacts
with the mechanics of the pore fluid and produces shear dependence
on fluid properties in the overall poroelastic system. The analysis
shows, for example, that this effect is always present (though sometimes
small in magnitude) in the systems studied, and can be quite large
(up to a definite maximum increase of 20 per cent)
in some rocks - including Spirit River sandstone and
Schuler-Cotton Valley sandstone.
|
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)