




Next: Stiffness formulation
Up: Compliance formulation
Previous: Case II. A* - A*/2
This case is the most general one of the three, and the one
we will study at greater length in the remainder of this discussion.
We want to understand how the introduction of liquid into the pore
space affects the shear modulus. We also want to know how the
anisotropy influences, i.e., aids or hinders, the impact of the
liquid on the shear behavior. To achieve this understanding, it
should be sufficient to consider the case when
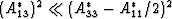 , assuming as we do that both
factors are nonzero. Then, expanding the square root in
(19), we have
, assuming as we do that both
factors are nonzero. Then, expanding the square root in
(19), we have
| 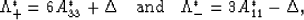 |
(25) |
where 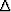 is defined consistently by either of the two preceeding
expressions or by
is defined consistently by either of the two preceeding
expressions or by
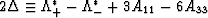 and is also given approximately for cases of interest here by
and is also given approximately for cases of interest here by
| 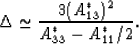 |
(26) |
In the quasi-isotropic soft anisotropy limit under consideration, we find
| ![\begin{eqnarray}
\Delta \simeq
{{2(\beta_1-\beta_3)^2(2\beta_1+\beta_3)^2/27\gam...
...{
\nu/E +[(2\beta_1+\beta_3)^2 -2(\beta_1-\beta_3)^2]/9\gamma}}.
\end{eqnarray}](img76.gif) |
(27) |
All of the mechanical effects of the liquid that contribute to this formula
appear in the factor 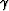 . The order at which
. The order at which
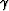 appears depends on the relative importance of the two terms
in the denominator of this expression. If the second term ever dominates,
then one factor of
appears depends on the relative importance of the two terms
in the denominator of this expression. If the second term ever dominates,
then one factor of 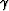 cancels, and therefore
cancels, and therefore
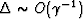 , and furthermore
, and furthermore 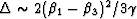 if
if 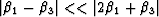 . If instead what seems to be the more
likely situation
holds and the first term in the denominator dominates, then
. If instead what seems to be the more
likely situation
holds and the first term in the denominator dominates, then 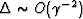 . So in either of these cases, as long as
. So in either of these cases, as long as 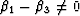 (which is the condition for soft anisotropy),
we always have contributions to
(which is the condition for soft anisotropy),
we always have contributions to  from liquid mechanical
effects. There do not appear to be any combinations of the parameters
for which the fluid effects disappear whenever the material is in
the class of anisotropic solids considered here.
from liquid mechanical
effects. There do not appear to be any combinations of the parameters
for which the fluid effects disappear whenever the material is in
the class of anisotropic solids considered here.





Next: Stiffness formulation
Up: Compliance formulation
Previous: Case II. A* - A*/2
Stanford Exploration Project
5/23/2004
![]() , assuming as we do that both
factors are nonzero. Then, expanding the square root in
(19), we have
, assuming as we do that both
factors are nonzero. Then, expanding the square root in
(19), we have