Pseudo-primary from multiples

We can generate pseudo-primary shot gathers W by computing:  

$$W(x_p,x_m,\omega)=\sum_{x_s} M(x_s, x_m,\omega)\bar{P}(x_s,x_p,\omega),$$ (1)

where $\omega$ is the frequency, x_s is the shot location, $\bar{P}(x_s,x_p,\omega)$ is the complex conjugate of the original trace recorded at the surface location x_p, and $M(x_s, x_m,\omega)$ is the multiple reflection data recorded at the surface location x_m. In equation (1), note that first-order multiples in M are transformed into primaries (cross-correlation with primaries in P) and zero-lag components (cross-correlation with first-order multiples in P) in the pseudo-primaries W. Similarly, second-order multiples in M are transformed into primaries (cross-correlation with first-order multiple in P), first-order multiples (cross-correlation with the primaries in P) and zero-lag components (cross-correlation with second-order multiples in P) in the pseudo-primaries W, and so on.

In contrast to primaries in the original dataset, pseudo-primaries can illuminate different areas at different angles. They contain subsurface information that primaries do not. Because of recording geometries, it is often difficult to obtain near-offset data, as well as far-offset data. Pseudo-primaries created from multiples can help fill these acquisition holes.

 

nearoffset
Figure 2 Near-offset recovery example : In (a), no trace is recorded at x_m for the shot at x_p. In (b), a primary reflection is recorded at x_p and a multiple reflection is recorded at x_m for the shot at x_s. With the pseudo-primaries, we recover the trace with a source at x_p and receiver at x_m.

 

faroffset
Figure 3 Far-offset recovery example: In (a), no trace is recorded at x_m, since it is outside the acquisition spread for the shot at x_p. In (b), both x_p and x_m are within the acquisition spread for the shot at x_s. A primary reflection is recorded at x_p and a multiple reflection is recorded at x_m. With the pseudo-primaries, we recover the trace with a source at x_p and receiver at x_m.

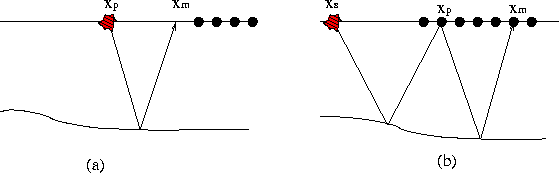
Figure 2 illustrates how missing near-offset traces are recovered in the pseudo-primary dataset. In Figure 2a, near offsets are missing when the source is at x_p. In Figure 2b, the primary reflection is recorded at x_p and the multiple reflection is recorded at x_m for the shot at x_s. By cross-correlating the traces at x_p and x_m in Figure 2b, we obtain the pseudo-primary trace, whose shot and receiver locations are x_p and x_m, respectively. So the near-offset missing trace is recovered in the pseudo-primaries.

Figure 3 illustrates how missing far-offsets are recovered by the pseudo-primary dataset in some special cases. Using reciprocity, we can obtain the negative-offset data by mirroring sources and receivers. In Figure 3a, the primary reflection with a source at x_p and receiver at x_m is outside the acquisition spread. In Figure 3b, a primary reflection is recorded at x_p and a multiple reflection is recorded at x_m for the shot at x_s. Both x_p and x_m are within the acquisition spread. By cross-correlating the traces at x_p and x_m in Figure 3b, we obtain a trace of the pseudo-primaries, whose shot and receiver locations are x_p and x_m, respectively. So the far-offset missing trace is recovered with pseudo-primaries. Note that to recover the far-offset trace, as is illustrated in Figure 3, we need a steeply dipping reflector.

We now illustrate our technique on the Sigsbee2B dataset. Figure 4 shows four shot gathers with a source at 50,000 ft: (a) the original dataset (primaries + multiples) with near and far offsets removed, (b) the surface-related multiples with near and far offsets removed, (c) the original dataset (primaries + multiples) with full offsets, and (d) the pseudo-primary dataset.

We mirrored the sources and receivers to get negative offsets. To demonstrate that pseudo-primaries can interpolate data inside the acquisition holes, we removed the offsets that are less than 2,000 ft and greater than 20,000 ft from the original dataset and the surface-related multiples, which are illustrated in Figure 4a and 4b. Figure 4d shows the pseudo-primary shot gather obtained by cross-correlating the original dataset with the multiple dataset without near and far offsets. Comparing the original shot gather in Figure 4c (no mute) with the pseudo-primary shot gather in Figure 4d, we conclude that the pseudo-primary shot gather is very similar to the original shot gather. Note that some artifacts and noisy events appear in the pseudo-primary gather. The noise arises during the cross-correlation of unpaired events at different surface locations. It might be better handled by the method of Berkhout and Verschuur (2003). The near-offset data are recovered very well in the pseudo-primary gather. For far offsets, notice that the event in the oval of Figure 4c, which is removed in Figure 4a, is recovered in Figure 4d. We think that this far-offset event is recovered in the pseudo-primary gather due to the presence of two large canyons with steeply dipping walls on the salt body (Figure 1), similar to the structure illustrated in Figure 3. Note that more shots would help to recover more events at far offsets in Figure 4d.

Figure 5 compares the original zero-offset dataset with the pseudo-primary zero-offset dataset. Same as Figure 4, the pseudo-primary dataset is generated by cross-correlating the original dataset with the multiple dataset without near and far offsets. These two zero-offset datasets have similar structures.

 

shotgather
Figure 4 Comparison of shot gathers at 50,000 ft for (a) the original dataset (primaries + multiples) with near and far offsets removed, (b) surface-related multiples with near and far offsets removed, (c) the original dataset (primaries + multiples) with full offsets, and (d) the pseudo-primary, generated by cross-correlating the original dataset with the multiple dataset without near and far offsets.

 

zerooffset
Figure 5 Comparison of zero-offset datasets for (a) the original data (primaries+multiples) and (b) the pseudo-primary, generated by cross-correlating the original dataset with the multiple dataset without near and far offsets.