Kinematic properties of 3-D ADCIGs

Biondi and Symes (2003) analyze in detail the kinematic properties of 2-D ADCIGs when the migration velocity is not correct. Their analysis can be extended to 3-D by following the same geometrical considerations we used in the previous sections to generalize ADCIGs from 2-D to 3-D (Figure 3). However, there is an important conceptual difference between the 2-D case and the 3-D case. In 2-D we can assume that the source and receiver rays cross even when the data were migrated with the wrong velocity; below the imaging point in case of too low migration velocity and above the imaging point in the opposite case. 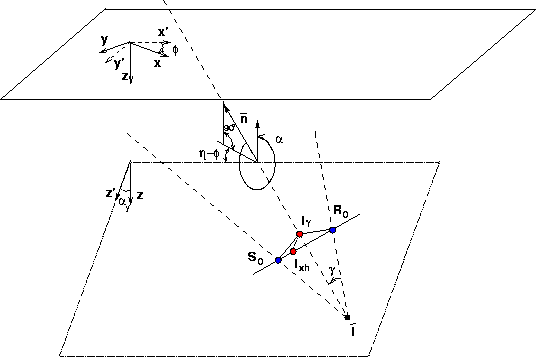In 3-D, this assumption is easily violated because two rays are not always coplanar. Fortunately, the plane-wave interpretation is still valid and the plane of coplanarity of Figure 13 is determined by the coplanarity condition expressed in equation (10) applied to the phase vectors of the incident and reflected plane waves, or, alternatively by the coplanarity condition expressed in equation (18) applied to the offset dips present in the prestack image. The source and receiver plane waves constructively interfere along an imaging line; the angle-domain image point $\bf{{I}_{\gamma}}$is defined as the intersection of this imaging line with the tilted plane of coplanarity. Once this plane is defined, the geometrical relations between the objects (rays and imaging points) that lie on the vertical plane in 2-D Biondi and Symes (2003), directly apply to 3-D on the tilted plane of coplanarity, as it is schematically represented in Figure 13. In particular, the relative position of the angle-domain image point $\bf{{I}_{\gamma}}$and of the crossing point between the source and receiver ray $\bf{\bar{I}}$ are defined on the tilted plane. The 2-D results translate into the following 3-D results:

1.

The transformation to the angle domain shifts the image point along the tilted vertical direction z' from the offset-domain image point $\bf{I_{x_h}}$ to the angle-domain image point $\bf{{I}_{\gamma}}$.

2.

$\bf{{I}_{\gamma}}$lies on the normal to the apparent geological dip passing through the crossing point of the source and receiver rays ($\bf{\bar{I}}$). $\bf{{I}_{\gamma}}$ is located at the crossing point of the lines passing through $\bf{S_0}$ and $\bf{R_0}$and orthogonal to the source ray and receiver ray, respectively.

3.

From the previous geometric results, by invoking Fermat's principle and applying simple trigonometry, we can also easily derive a relationship between the total normal shift ${\bf \Delta n}_{\rm tot}=\left(\bf{{I}_{\gamma}}-\bf{\bar{I}}\right)$ and the total traveltime perturbation caused by velocity errors as follows:  

$${\bf \Delta n}_{\rm tot}= \frac{\Delta t}{2 S\cos\gamma} {\bf n},$$ (19)

where S is the background slowness around the image point and $\Delta t$ is defined as the difference between the perturbed traveltime and the background traveltime.

These results are based on the assumption that the velocity is locally smooth in a neighborhood of the imaging point. Furthermore, the relationship expressed in equation (19) depends on the assumption of stationary raypaths, since we need to invoke Fermat's principle. We can assume stationary raypaths if the velocity perturbations are small. Biondi and Symes (2003) discuss these assumptions in details.

The relationship expressed in equation (19) forms the basis of using ADCIGs for MVA. Similar relationships have been extensively used in MVA methods based on constant-offset Kirchhoff migration Etgen (1990); Meng et al. (1999a,b); Stork (1992). Equation (19) can be directly used to transform measurements of depth errors in ADCIGs into traveltime perturbations that can be inverted by a ray-based tomographic inversion; or it can be the foundation for the derivation of accurate RMO functions to be applied to measure depth errors in ADCIGs.

 

cig-3d-mva-v5
Figure 13 Geometry of an ADCIG for a single event migrated with the wrong velocity. The transformation to the angle domain shifts the offset-domain image point $\bf{I_{x_h}}$to the angle-domain image point $\bf{{I}_{\gamma}}$.Both image points lie on the tilted plane of coplanarity.