 |
Regardless of whether they have been computed using source-receiver
migration or shot-profile migration,
ADCIGs computed before imaging have the same geometrical interpretation.
Strictly speaking,
they are functions of the offset ray parameters (pxh,pyh)
and not of the reflection opening angle ![]() and the reflection azimuth
and the reflection azimuth ![]() .However, the offset ray parameters (pxh,pyh)
are easily related to
.However, the offset ray parameters (pxh,pyh)
are easily related to ![]() and
and ![]() by simple trigonometric relationships.
We now derive these relationships,
starting from the simpler 2-D case.
The understanding gained from the 2-D analysis
will help the analysis of the more complex 3-D case.
by simple trigonometric relationships.
We now derive these relationships,
starting from the simpler 2-D case.
The understanding gained from the 2-D analysis
will help the analysis of the more complex 3-D case.
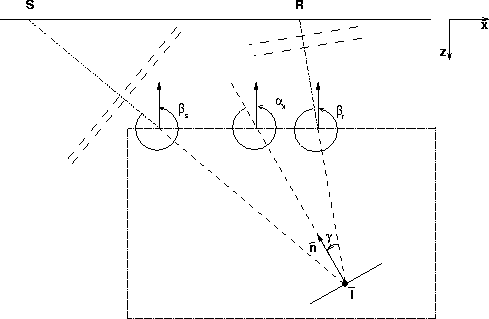
The schematic in Figure 2
defines the angles relevant to 2-D ADCIGs:
the reflection opening angle ![]() and
the geological dip angle
and
the geological dip angle ![]() ,which is defined as the angle formed by the vertical direction
and the normal to the apparent geological dip
,which is defined as the angle formed by the vertical direction
and the normal to the apparent geological dip ![]() ,both oriented in the upward direction.
The box
in Figure 2
signifies that for the purpose of our discussion
the geometric relationships are local around
the imaging point
,both oriented in the upward direction.
The box
in Figure 2
signifies that for the purpose of our discussion
the geometric relationships are local around
the imaging point ![]() .
.
The opening angle and the dip angle are
related to the source and receiver rays (plane waves)
propagation angles
![]() by the following simple relationships:
by the following simple relationships:
| |
(6) |
| |
(7) |
| |
(8) |
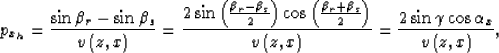 |
(9) |
The relationship in equation (9)
is also valid in 3-D when the reflection azimuth ![]() is equal to zero.
But in the general 3-D case we need to add another relationship
linking the cross-line offset ray parameter
pyh
to pxh and the angles
is equal to zero.
But in the general 3-D case we need to add another relationship
linking the cross-line offset ray parameter
pyh
to pxh and the angles ![]() and
and ![]() at the reflection point.
To derive this relationship,
we impose the constraint that
the source and the receiver rays must become coplanar
before meeting at the reflection point.
We will thus refer to this relationship
as the
coplanarity condition.
at the reflection point.
To derive this relationship,
we impose the constraint that
the source and the receiver rays must become coplanar
before meeting at the reflection point.
We will thus refer to this relationship
as the
coplanarity condition.
The coplanarity of the two rays
also simplifies the 3-D geometry of ADCIGs
and enables us to generalize
the 2-D geometric interpretation
in a straightforward manner.
The schematic in Figure 3
is the 3-D generalization of the 2-D schematic
shown in Figure 2.
The plane that is shared by the two rays in 3-D
corresponds to the vertical plane in 2-D.
As for Figure 2,
all the geometric relationships represented
in Figure 3 are local
in a neighborhood of the image point ![]() .This locality implies that
the source and receiver rays (plane waves)
need to satisfy the coplanarity condition
only at the image point,
not during propagation in the overburden.
.This locality implies that
the source and receiver rays (plane waves)
need to satisfy the coplanarity condition
only at the image point,
not during propagation in the overburden.
 |
We define the reflection azimuth angle
![]() as
the angle formed by the in-line axis x
with the line defined by the intersection of the plane of coplanarity
with a constant depth plane.
After rotation by
as
the angle formed by the in-line axis x
with the line defined by the intersection of the plane of coplanarity
with a constant depth plane.
After rotation by ![]() ,the horizontal coordinates x and y
become x' and y', respectively.
Once rotated by
,the horizontal coordinates x and y
become x' and y', respectively.
Once rotated by ![]() ,the plane of coplanarity is tilted with
respect to the vertical by
the cross-line dip angle
,the plane of coplanarity is tilted with
respect to the vertical by
the cross-line dip angle
![]() .All the angles
in
Figure 2
that are formed between the ray (plane wave) directions
and the true vertical axis z
(
.All the angles
in
Figure 2
that are formed between the ray (plane wave) directions
and the true vertical axis z
(![]() ,
, ![]() , and
, and ![]() )are now relative to the tilted vertical axis z';
these angles have the same meaning on the tilted plane
as they have on the vertical plane in 2-D.
Furthermore, the horizontal ray parameters
)are now relative to the tilted vertical axis z';
these angles have the same meaning on the tilted plane
as they have on the vertical plane in 2-D.
Furthermore, the horizontal ray parameters
![]() are not affected by the tilt,
since they depend on the angles formed by the rays
with the x axis.
In contrast, the angles
are not affected by the tilt,
since they depend on the angles formed by the rays
with the x axis.
In contrast, the angles ![]() ,
, ![]() ,
,
![]() , and
, and ![]() are affected by the rotation of the horizontal axes
by
are affected by the rotation of the horizontal axes
by ![]() ;we include the prime in the notation
to indicate the angles after rotation.
;we include the prime in the notation
to indicate the angles after rotation.
Imposing the coplanarity of
the source and receiver rays
along a plane rotated by
![]() with respect to the original
coordinate system provides us with the
needed relationship that constraints the
cross-line offset ray parameter py'h.
For the azimuth of the plane of coplanarity to be
with respect to the original
coordinate system provides us with the
needed relationship that constraints the
cross-line offset ray parameter py'h.
For the azimuth of the plane of coplanarity to be ![]() ,the ``rotated'' source and receiver ray-parameters
px's, py's, px'g, py'g
must be related by the following
expression:
,the ``rotated'' source and receiver ray-parameters
px's, py's, px'g, py'g
must be related by the following
expression:
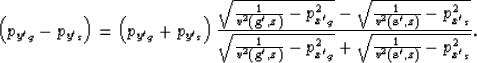 |
(10) |
This relationship was derived by Biondi and Palacharla (1996) to define common-azimuth migration, and it is demonstrated in the Appendix of their paper.
So far we have interpreted the coplanarity condition
in terms of source and receiver rays,
but it has a similar interpretation in terms of plane waves.
The phase vectors of two arbitrary plane waves are coplanar
by construction, since they meet at the origin.
The tilt angle ![]() and the azimuth
and the azimuth ![]() of the plane of coplanarity
for the incident and the reflected plane waves
are implicitly determined by
the coplanarity condition expressed in equation (10).
The cross-correlation of the two plane waves does not define
an imaging point but an imaging line
that is orthogonal to the plane of coplanarity.
The tilted plane shown in
Figure 3 is an arbitrary plane
parallel to the plane of coplanarity and the imaging point
of the plane of coplanarity
for the incident and the reflected plane waves
are implicitly determined by
the coplanarity condition expressed in equation (10).
The cross-correlation of the two plane waves does not define
an imaging point but an imaging line
that is orthogonal to the plane of coplanarity.
The tilted plane shown in
Figure 3 is an arbitrary plane
parallel to the plane of coplanarity and the imaging point ![]() is the intersection of the imaging line with this plane.
The source and receiver rays are defined
as the lines parallel to the phase vectors of
the corresponding plane waves
and passing through the imaging point
is the intersection of the imaging line with this plane.
The source and receiver rays are defined
as the lines parallel to the phase vectors of
the corresponding plane waves
and passing through the imaging point ![]() .
.
Using the relationships among the in-line ray parameters
expressed in equations (7)
(and their analogues along the cross-line direction y),
and equations (8),
and after applying trigonometric identities,
we can rewrite equation (10)
as a function of the local velocity ![]() and the angles
and the angles ![]() ,
,![]() ,
,![]() and
and ![]() as follows:
as follows:
| |
(11) |
| |
(12) |
This mapping of the ray parameters into angles depends on both the local velocity and the geological dips. When the spatial velocity variations are significant and the geological structure is complex, unraveling this dependence might be a challenge because of the well known difficulties in reliably measuring rapidly changing local dips. For some applications this dependency does not cause difficulties. For example, in a ray-based MVA Clapp and Biondi (2000), there is no need to perform the mapping from ray parameters to angles, since ray parameters are adequate initial conditions for ray tracing. For other applications, the reflection angles are needed, and thus the mapping must be performed. When this mapping is difficult, it might be convenient to use the ADCIGs computed after imaging, which are presented in the next section. This kind of ADCIG circumvents the need to estimate local dips by transforming the image directly into angles.