




Next: About this document ...
Up: REFERENCES
Previous: Source wavefield downward extrapolation
The recursion in equation (6) can
be also written in matrix form as
| 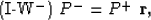 |
(16) |
| ![\begin{eqnarray}
\left[ \begin{array}
{cccccc}
{1} & {-{w}^{-}(z_0,z_i)} & 0 &....
...c}
0\\ p^-_r(z_i)\\ 0\\ ...\\ 0 \end{array} \right], \nonumber
\end{eqnarray}](img38.gif) |
(17) |
| |
where
- W- is a upper bidiagonal matrix containing the upward continuation
operator for all depth levels,
- P- is a column vector containing the receiver wavefield at all depth levels,
- P+ is a diagonal square matrix containing the source wavefield at all depth
levels, and
-
 is the reflectivity at all depth levels.
is the reflectivity at all depth levels.
Equation (16) represents the upward continuation
recursion written for a given frequency. We can write a similar
relationship for each of the frequencies in the data, and
group them all in a matrix relationship:
| 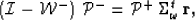 |
(18) |
where
-
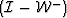 is a upper bidiagonal matrix containing the upward continuation
operators for all the frequencies in the data,
is a upper bidiagonal matrix containing the upward continuation
operators for all the frequencies in the data,
-
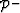 is a column vector containing the receiver wavefield for all
the frequencies,
is a column vector containing the receiver wavefield for all
the frequencies,
-
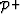 is a diagonal square matrix containing the source wavefield for all
the frequencies,
is a diagonal square matrix containing the source wavefield for all
the frequencies,
- and
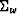 is the sum over frequency matrix with dimensions
is the sum over frequency matrix with dimensions 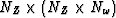 (the transpose of the spreading over frequencies),
(the transpose of the spreading over frequencies),
Equation (18) represents the upward continuation
recursion written for a given shot position. We can write a similar
relationship for each of the shot positions in the data, and
group them all in a matrix relationship:
| 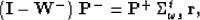 |
(19) |
where
-
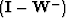 is a upper bidiagonal matrix containing the upward continuation
operators for all the shots in the data,
is a upper bidiagonal matrix containing the upward continuation
operators for all the shots in the data,
-
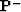 is a column vector containing the receiver wavefield for all the shots,
is a column vector containing the receiver wavefield for all the shots,
-
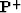 is a diagonal square matrix containing the source wavefield for all
the shots,
is a diagonal square matrix containing the source wavefield for all
the shots,
- and
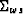 is the sum over the frequency matrix with dimensions
is the sum over the frequency matrix with dimensions 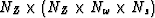 (the transpose of the spreading over frequencies),
(the transpose of the spreading over frequencies),





Next: About this document ...
Up: REFERENCES
Previous: Source wavefield downward extrapolation
Stanford Exploration Project
5/23/2004
![\begin{eqnarray}
\left[ \begin{array}
{cccccc}
{1} & {-{w}^{-}(z_0,z_i)} & 0 &....
...c}
0\\ p^-_r(z_i)\\ 0\\ ...\\ 0 \end{array} \right], \nonumber
\end{eqnarray}](img38.gif)
![\begin{eqnarray}
({\mathcal I}-{\mathcal W}^{-})=\left[ \begin{array}
{cccc}
{ I...
.....& { I- W^-(\omega_{N_{\omega}})} \end{array} \right], \nonumber
\end{eqnarray}](img42.gif)
![\begin{eqnarray}
{\mathcal P}^-=\left[ \begin{array}
{cccc}
P^-(\omega_1)\\ P^...
...)\\ ...\\ P^-(\omega_{N_\omega}) \end{array} \right], \nonumber
\end{eqnarray}](img44.gif)
![\begin{eqnarray}
{\mathcal P}^+=\left[ \begin{array}
{cccc}
{ P^+(\omega_1)} & 0...
...& 0 &...& {P^+(\omega_{N_\omega})} \end{array} \right], \nonumber
\end{eqnarray}](img45.gif)
![\begin{eqnarray}
\Sigma_\omega = \left[ \left\vert \begin{array}
{cccc}
{1} & 0 ...
..... \\ 0 & 0 &...& {1} \end{array} \right\vert\right]. \nonumber
\end{eqnarray}](img48.gif)
![\begin{eqnarray}
\left( {\bf I} - {\bf W}^{-} \right)=\left[ \begin{array}
{cccc...
...thcal I- \mathcal W}^{-}(s_{N_s})} \end{array} \right], \nonumber
\end{eqnarray}](img51.gif)
![\begin{eqnarray}
{\bf P}^-=\left[ \begin{array}
{cccc}
{\mathcal P}^-(s_1)\\ {...
...\\ ...\\ {\mathcal P}^-(s_{N_s}) \end{array} \right], \nonumber
\end{eqnarray}](img52.gif)
![\begin{eqnarray}
{\bf P}^+=\left[ \begin{array}
{cccc}
{ {\mathcal P}^+(s_1)} & ...
...& 0 &...& {{\mathcal P}^+(s_{N_s})} \end{array}\right], \nonumber
\end{eqnarray}](img53.gif)
![\begin{eqnarray}
\Sigma_{\omega s} = \left[ \left\vert \begin{array}
{cccc}
{1} ...
..... \\ 0 & 0 &...& {1} \end{array} \right\vert\right]. \nonumber
\end{eqnarray}](img56.gif)