




Next: Receiver wavefield extrapolation
Up: REFERENCES
Previous: REFERENCES
The recursion in equations (2) and (3) can
be also written in matrix form as
| 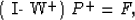 |
(13) |
where
- W+ is a lower bidiagonal matrix containing the downward continuation
operator for all depth levels,
- P+ is a column vector containing the source wavefield at all depth
levels, and
- F is a column vector containing the source signature.
Equation (13) represents the downward continuation
recursion written for a given frequency. We can write a similar
relationship for each of the frequencies in the data, and
group them all in a matrix relationship:
| 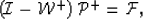 |
(14) |
where
-
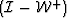 is a lower bidiagonal matrix containing the downward continuation
operators for all the frequencies in the data,
is a lower bidiagonal matrix containing the downward continuation
operators for all the frequencies in the data,
-
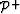 is a column vector containing the wavefield data for all
the frequencies, and
is a column vector containing the wavefield data for all
the frequencies, and
-
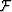 is a column vector containing the source signature for all
the frequencies.
is a column vector containing the source signature for all
the frequencies.
Equation (14) represents the downward continuation
recursion written for a given shot position. We can write a similar
relationship for each of the shot positions in the data, and
group them all in a matrix relationship:
| 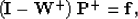 |
(15) |
where
-
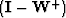 is a lower bidiagonal matrix containing the downward continuation
operators for all the shots in the data,
is a lower bidiagonal matrix containing the downward continuation
operators for all the shots in the data,
-
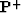 is a column vector containing the wavefield data for all
the shots, and
is a column vector containing the wavefield data for all
the shots, and
-
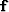 is a column vector containing the source signature for all
the shots.
is a column vector containing the source signature for all
the shots.
B





Next: Receiver wavefield extrapolation
Up: REFERENCES
Previous: REFERENCES
Stanford Exploration Project
5/23/2004
![\begin{eqnarray}
\left[ \begin{array}
{cccccc}
{1} & 0 & 0 &...& 0 & 0 \\ {-w^+...
...ay}
{ccccc}
f\\ 0\\ 0\\ ...\\ 0 \end{array} \right], \nonumber
\end{eqnarray}](img28.gif)
![\begin{eqnarray}
\left[ \begin{array}
{cccc}
{ I- W^+(\omega_1)} & 0 &...& 0 \\ ...
..._2)\\ ...\\ F(\omega_{N_\omega}) \end{array} \right], \nonumber
\end{eqnarray}](img30.gif)
![\begin{eqnarray}
\left[ \begin{array}
{cccc}
{ {\mathcal I- \mathcal W}^+(s_1)} ...
...2)\\ ...\\ {\mathcal F}(s_{N_s}) \end{array} \right], \nonumber
\end{eqnarray}](img35.gif)