![\begin{displaymath}
0.15in]
\begin{tabular}
{\vert c\vert c\vert c\vert c\vert c...
... 0.118 & 34.5 & 1.65 & 0.017 & 0.354\\ hline\hline\end{tabular}\end{displaymath}](img78.gif)
To illustrate the use of the formulas derived for the coefficients of the double-porosity system, we will now compute and plot the coefficients for a realistic system. We will use data of Coyner (1984) for Navajo sandstone, and modify it somewhat to produce a plot that will highlight the results obtained from the equations. The first problem we encounter in doing so is that, although we can make reasonable direct estimates of the bulk and shear moduli of the constituents, we also must have an estimate of the overall bulk modulus K* of the composite double-porosity medium. And more than that, we need it as a function of the volume fractions of the two constituents. Our analysis has assumed that K* was given or measured independently. For present purposes, it is sensible to use an effective medium theory such as the symmetric self-consistent method [or CPA = coherent potential approximation -- see Berryman and Berge (1996) for a discussion and references therein for elaboration] to estimate K*. The CPA has the advantage that it treats both constituents equally (i.e., symmetrically) and therefore does not assume that one constituent always surrounds the other -- so there is no host material [see Berge et al. (1993) for further discussion]. With this addition to the theory, we can proceed to the calculations.
![\begin{displaymath}
0.15in]
\begin{tabular}
{\vert c\vert c\vert c\vert c\vert c...
... 0.118 & 34.5 & 1.65 & 0.017 & 0.354\\ hline\hline\end{tabular}\end{displaymath}](img78.gif)
The parameters used for Navajo sandstone are listed in Table 1.
Although Poisson's ratio ![]() does not appear explicitly in the equations
here, it is required in the CPA (or any but the most elementary)
effective medium calculation for the overall bulk modulus K*.
The results are shown in Figure 3.
does not appear explicitly in the equations
here, it is required in the CPA (or any but the most elementary)
effective medium calculation for the overall bulk modulus K*.
The results are shown in Figure 3.
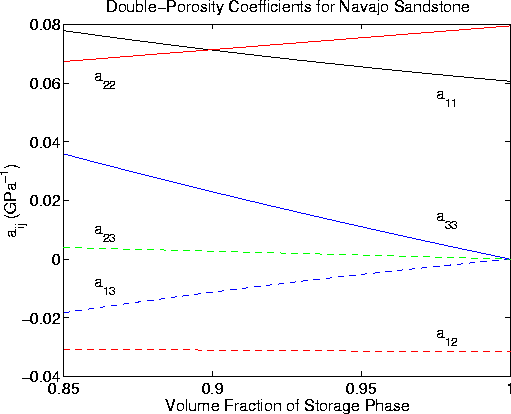 |
Note that the off-diagonal coefficient a23, which couples the fluid in the storage porosity to the fluid in the transport porosity, is very close to zero for all values of storage material volume fraction. This behavior has been observed previously (Berryman and Wang 1995), and is believed to be a strong indication that the double-porosity approach is appropriate for the system studied. If this coefficient is not small, then the fluids in the two types of porosity are strongly coupled and therefore should not be treated as a double-porosity system.
The behavior of the other coefficients is as one would expect: All the coefficients for the transport porosity tend to vanish as the volume fraction of this phase vanishes, and the medium again reduces to a single-porosity system in this limit.