




Next: Example
Up: Berryman: Double-porosity analysis
Previous: Generalized Biot-Willis parameters
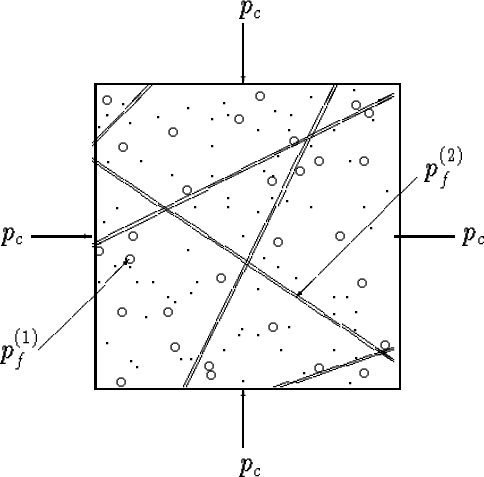
Figure 2:
A composite porous medium is composed of two distinct
types of porous solid (1,2).
In the model illustrated here and treated in the text,
the two types of materials are well-bonded but
themselves have very different porosity types, one being a storage
porosity (type-1) and the other (type-2) being a transport porosity
(and therefore fracture-like, or tube-like as illustrated in
cross-section in this diagram).
 |
Several of the main results obtained previously can be derived
in a more elegant fashion by using a new
self-similar (uniform expansion) thought experiment.
The basic idea we are going to introduce here is
analogous to, but nevertheless distinct from,
other thought experiments used in thermoelasticity
by Cribb (1968) and in single-porosity poroelasticity
by Berryman and Milton (1991) and Berryman and Pride (1998).
Cribb's method provided an independent and simpler derivation of
Levin's (1967) results on thermoelastic expansion coefficients.
The present results also provide an independent and simpler
derivation of results obtained recently by Berryman and Pride (2002)
for the double-porosity coefficients.
Related methods in micromechanics are sometimes called
``the method of uniform fields'' by some authors
(Dvorak and Benveniste, 1997).
We have already shown that a11 = 1/K*.
We will now show how to determine the remaining five constants
in the case of a binary composite system, such as that illustrated in
Figure micropic. The components of the
system are themselves porous materials 1 and 2, but each is assumed to
be what we call a ``Gassmann material'' satisfying
[in analogy to equation (all)]
| 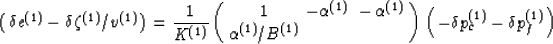 |
(24) |
for material 1 and a similar expression for material 2.
The new constants appearing on the right are the drained bulk modulus
K(1) of material 1, the corresponding Biot-Willis parameter
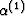 , and the Skempton coefficient B(1).
The volume fraction v(1) appears here to correct for the
difference between a global fluid content and the corresponding
local variable for material 1.
The main special characteristic of a Gassmann porous material
is that it is composed of only one type of solid constituent,
so it is ``microhomogeneous'' in its solid component, and
in addition the porosity
is randomly, but fairly uniformly, distributed so there is a
well-defined constant porosity
, and the Skempton coefficient B(1).
The volume fraction v(1) appears here to correct for the
difference between a global fluid content and the corresponding
local variable for material 1.
The main special characteristic of a Gassmann porous material
is that it is composed of only one type of solid constituent,
so it is ``microhomogeneous'' in its solid component, and
in addition the porosity
is randomly, but fairly uniformly, distributed so there is a
well-defined constant porosity 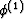 associated with material 1, etc.
associated with material 1, etc.
For our new thought experiment, we ask the question: Is it possible to
find combinations of 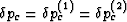 ,
,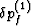 , and
, and 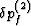 such that the expansion or
contraction of the system is spatially uniform or self-similar?
This is the same as asking if we can find uniform
confining pressure
such that the expansion or
contraction of the system is spatially uniform or self-similar?
This is the same as asking if we can find uniform
confining pressure 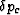 , and pore-fluid pressures
, and pore-fluid pressures
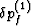 and
and 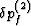 , such that
, such that
| 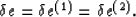 |
(25) |
If these conditions can all be met simultaneously,
then results for system constants
can be obtained purely algebraically without ever having to solve
the equilibrium equations for nonconstant stress and strain.
We have initially set 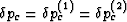 , as the
condition of uniform confining pressure is clearly necessary for this
self-similar thought experiment to achieve
a valid solution of the equilibrium equations.
, as the
condition of uniform confining pressure is clearly necessary for this
self-similar thought experiment to achieve
a valid solution of the equilibrium equations.
So, the first condition to be considered is the equality of
the strains of the two constituents:
| 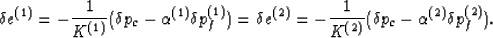 |
(26) |
If this condition can be satisfied, then the two constituents are
expanding or contracting at the same rate and it is clear that
self-similarity will prevail. If we imagine that 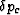 and
and
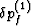 have been chosen, then we only need to choose
an appropriate value of
have been chosen, then we only need to choose
an appropriate value of 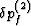 , so that (e1e2) is
satisfied. This requires that
, so that (e1e2) is
satisfied. This requires that
| 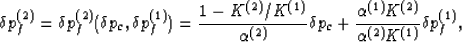 |
(27) |
which shows that, except for some very special choices of the material
parameters (such as 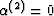 ),
),
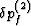 can in fact always be chosen so the
uniform expansion takes place. (We are not considering long-term
effects here. Clearly, if the pressures are left to themselves, they
will tend to equilibrate over time so that
can in fact always be chosen so the
uniform expansion takes place. (We are not considering long-term
effects here. Clearly, if the pressures are left to themselves, they
will tend to equilibrate over time so that 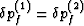 .We are considering only the ``instantaneous'' behavior of the material
permitted by our system of equations and finding what internal consistency
of this system of equations implies must be true.)
.We are considering only the ``instantaneous'' behavior of the material
permitted by our system of equations and finding what internal consistency
of this system of equations implies must be true.)
Using formula (pf2), we can now eliminate 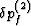 from
the remaining equality so that
from
the remaining equality so that
| 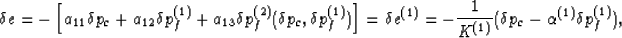 |
(28) |
where 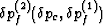 is given by (pf2).
Making the substitution and then noting that
is given by (pf2).
Making the substitution and then noting that 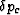 and
and
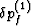 were chosen independently and arbitrarily,
we see that the resulting coefficients of these two variables
must each vanish. The equations we obtain in this way are
were chosen independently and arbitrarily,
we see that the resulting coefficients of these two variables
must each vanish. The equations we obtain in this way are
| 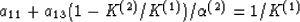 |
(29) |
and
| 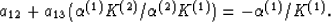 |
(30) |
Since a11 is known, equation (fora13) can be solved directly for
a13, giving
| 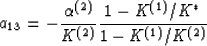 |
(31) |
Similarly, since a13 is now known, substituting into (fora12)
gives
| 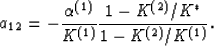 |
(32) |
Thus, three of the six coefficients have been determined.
To evaluate the remaining three coefficients, we must consider what
happens to the fluid increments during the same self-similar expansion
thought experiment. We will treat only material 1, but the
equations for material 2 are completely analogous.
>From the preceding equations, it follows that
| ![\begin{displaymath}
\delta\zeta^{(1)} = a_{12}\delta p_c + a_{22} \delta p_f^{(1...
...)}\delta p_c +
(\alpha^{(1)}/B^{(1)})\delta p_f^{(1)}\right].
\end{displaymath}](img69.gif) |
(33) |
Again substituting for 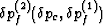 from
(pf2) and noting once more that the resulting equation contains
arbitrary values of
from
(pf2) and noting once more that the resulting equation contains
arbitrary values of 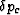 and
and 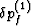 , so that the
coefficients of these terms must vanish separately, gives two equations
, so that the
coefficients of these terms must vanish separately, gives two equations
| 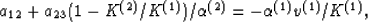 |
(34) |
and
| 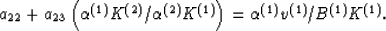 |
(35) |
Solving these equations in sequence as before, we obtain
| ![\begin{displaymath}
a_{23} = {{K^{(1)}K^{(2)}\alpha^{(1)}\alpha^{(2)}}\over{(K^{...
...{(1)}}} + {{v^{(2)}}\over{K^{(2)}}}
- {{1}\over{K^*}}\right],
\end{displaymath}](img72.gif) |
(36) |
and
| ![\begin{displaymath}
a_{22} = {{v^{(1)}\alpha^{(1)}}\over{B^{(1)}K^{(1)}}}
- \lef...
...{(1)}}} + {{v^{(2)}}\over{K^{(2)}}}
- {{1}\over{K^*}}\right].
\end{displaymath}](img73.gif) |
(37) |
Performing the corresponding calculation for 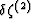 produces
formulas for a32 and a33. Since the formula in
(xa23) is already symmetric in the component indices, the formula
for a32 provides nothing new. The formula for a33 is easily
seen to be identical in form to a22, but with the 1 and 2 indices
interchanged everywhere.
produces
formulas for a32 and a33. Since the formula in
(xa23) is already symmetric in the component indices, the formula
for a32 provides nothing new. The formula for a33 is easily
seen to be identical in form to a22, but with the 1 and 2 indices
interchanged everywhere.
This completes the derivation of all five of the needed coefficients of
double porosity for the two constituent model.
These results can now be used to show how the constituent properties
K,  , B average at the macrolevel for a two-constituent
composite. We find
, B average at the macrolevel for a two-constituent
composite. We find
and
It should also be clear that parts of the preceding analysis generalize
easily to the multi-porosity problem. We discuss some of these
remaining issues in the final section.





Next: Example
Up: Berryman: Double-porosity analysis
Previous: Generalized Biot-Willis parameters
Stanford Exploration Project
6/8/2002


![]() ,
,![]() , and
, and ![]() such that the expansion or
contraction of the system is spatially uniform or self-similar?
This is the same as asking if we can find uniform
confining pressure
such that the expansion or
contraction of the system is spatially uniform or self-similar?
This is the same as asking if we can find uniform
confining pressure ![]() , and pore-fluid pressures
, and pore-fluid pressures
![]() and
and ![]() , such that
, such that
![]() from
the remaining equality so that
from
the remaining equality so that
![\begin{displaymath}
a_{23} = {{K^{(1)}K^{(2)}\alpha^{(1)}\alpha^{(2)}}\over{(K^{...
...{(1)}}} + {{v^{(2)}}\over{K^{(2)}}}
- {{1}\over{K^*}}\right],
\end{displaymath}](img72.gif)
![\begin{displaymath}
a_{22} = {{v^{(1)}\alpha^{(1)}}\over{B^{(1)}K^{(1)}}}
- \lef...
...{(1)}}} + {{v^{(2)}}\over{K^{(2)}}}
- {{1}\over{K^*}}\right].
\end{displaymath}](img73.gif)
![]() produces
formulas for a32 and a33. Since the formula in
(xa23) is already symmetric in the component indices, the formula
for a32 provides nothing new. The formula for a33 is easily
seen to be identical in form to a22, but with the 1 and 2 indices
interchanged everywhere.
produces
formulas for a32 and a33. Since the formula in
(xa23) is already symmetric in the component indices, the formula
for a32 provides nothing new. The formula for a33 is easily
seen to be identical in form to a22, but with the 1 and 2 indices
interchanged everywhere.
![]() , B average at the macrolevel for a two-constituent
composite. We find
, B average at the macrolevel for a two-constituent
composite. We find
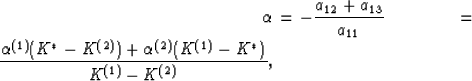
![\begin{eqnarray}
{{1}\over{B}} &=& - {{a_{22}+2a_{23}+a_{33}}\over{a_{12}+a_{13}...
...}}} + {{v^{(2)}}\over{K^{(2)}}}
- {{1}\over{K^*}}\right]\right).
\end{eqnarray}](img76.gif)