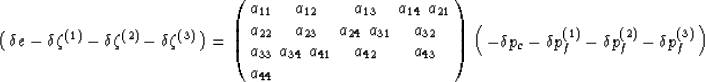
Micromechanical analysis provides definite answers to the question of how the coefficients in double-porosity systems are to be computed from knowledge of the constituents' properties. The question then naturally arises whether this analysis can be generalized to multi-porosity systems. Certainly, multi-porosity systems are the ones most likely to represent realistic systems occurring in nature, for example, oil and gas reservoirs. And, therefore, we need to address these issues. Transport in triple-porosity and multi-porosity systems have already been studied by some authors (Bai, Elsworth, and Roegiers 1993b; Bai and Roegiers, 1997), hence, it is timely to consider the geomechanical aspects of these problems. We will set up the problem and describe its general characteristics here, but the full solution will be left to future work.
The resulting coefficient matrices will clearly take a form analogous the ones already studied. For example, in a triple-porosity system, the macroscopic governing equations are:
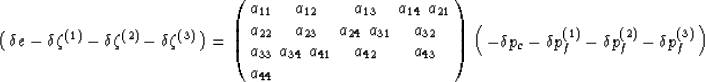 |
(38) |
In general, for an N-porosity system of the form considered here,
the total number of coefficients to be determined in the
![]() system of equations is N+1 diagonal and N(N+1)/2 unique off-diagonal
coefficients, for a total of G = (N+1)(N+2)/2 coefficients. And
the nature of a11 remains unchanged for any N.
If we assume that each of the unique porosities can be associated with
a Gassmann (microhomogeneous) material, then we have equations of the
same form as (Gassmannss1) for each of these constituents, and
therefore three mechanical coefficients plus the porosity of each
constituent is assumed to be known, at least approximately, in order
for this analysis to proceed. The uniform expansion/contraction
scenario
carries over to the multi-porosity system, but does not supply enough
equations to close the system by itself for N > 2. To see this,
note that once
system of equations is N+1 diagonal and N(N+1)/2 unique off-diagonal
coefficients, for a total of G = (N+1)(N+2)/2 coefficients. And
the nature of a11 remains unchanged for any N.
If we assume that each of the unique porosities can be associated with
a Gassmann (microhomogeneous) material, then we have equations of the
same form as (Gassmannss1) for each of these constituents, and
therefore three mechanical coefficients plus the porosity of each
constituent is assumed to be known, at least approximately, in order
for this analysis to proceed. The uniform expansion/contraction
scenario
carries over to the multi-porosity system, but does not supply enough
equations to close the system by itself for N > 2. To see this,
note that once ![]() and
and ![]() are chosen, then
all the remaining
are chosen, then
all the remaining ![]() 's are determined by the uniform strain
condition and Gassmann's relations.
Then, substituting these values into the multi-porosity system
[e.g., (tripleporosity)], we see there are always two
equations for each row of the matrix. This results in S = 2(N+1) equations
just from this self-similar thought experiment. These two sets of numbers are
compared in Table 2. In addition to these equations, we
always have the 3 conditions from the long-time limits, and we can
also find other
equations as needed by considering other experiments on the system
[e.g., see Berryman and Wang (1995)].
However, it is important to remember that it is the number of
linearly independent equations that is pertinent, and determining this
number has so far not proven to be a easy task for the general case.
At the present writing, closure of the system of equations for the
multi-porosity coefficients when N > 2 is an open question.
's are determined by the uniform strain
condition and Gassmann's relations.
Then, substituting these values into the multi-porosity system
[e.g., (tripleporosity)], we see there are always two
equations for each row of the matrix. This results in S = 2(N+1) equations
just from this self-similar thought experiment. These two sets of numbers are
compared in Table 2. In addition to these equations, we
always have the 3 conditions from the long-time limits, and we can
also find other
equations as needed by considering other experiments on the system
[e.g., see Berryman and Wang (1995)].
However, it is important to remember that it is the number of
linearly independent equations that is pertinent, and determining this
number has so far not proven to be a easy task for the general case.
At the present writing, closure of the system of equations for the
multi-porosity coefficients when N > 2 is an open question.
The analysis presented here has been strictly for isotropic constituents, and an isotropic overall multi-porosity system. Generalization to anisotropic systems is both possible and desirable, but the analysis obviously becomes more complex because of the proliferation of coefficients that results.
![\begin{displaymath}
0.15in]
\begin{tabular}
{\vert c\vert c\vert c\vert c\vert ...
...15 \hline
$S$\space & -- & 6 & 8 & 10 \hline\hline\end{tabular}\end{displaymath}](img81.gif)