




Next: About this document ...
Up: Clapp: Effect of velocity
Previous: AVA analysis
- Castagna, J. P., Swan, H. W., and Foster, D. J., 1998, Framework for AVO gradient and intercept interpretation: Geophysics, 63, no. 3, 948-956.
- Claerbout, J.
-
- Geophysical Estimation by Example: Environmental soundings image enhancement:.
http://sepwww.stanford.edu/sep/prof/, 1998.
- Clapp, R., 2000, Multiple realizations using standard inversion techniques: SEP-105, 67-78.
-
- Clapp, R. G., 2001a, Geologically constrained migration velocity analysis: Ph.D. thesis, Stanford University.
-
- Clapp, R. G., 2001b, Multiple realizations: Model variance and data uncertainty: SEP-108, 147-158.
-
- Gratwick, D., 2001, Amplitude analysis in the angle domain: SEP-108, 45-62.
-
- Guitton, A., 2000, Coherent noise attenuation using Inverse Problems and Prediction Error Filters: SEP-105, 27-48.
-
- Isaaks, E. H., and Srivastava, R. M., 1989, An Introduction to Applied Geostatistics: Oxford University Press.
-
- Sava, P., 2000, Variable-velocity prestack Stolt residual migration with application to a North Sea dataset: SEP-103, 147-157.
-
A
We can follow a parallel definition for the data fitting goal in
terms of the inverse noise covariance 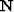 :
:
| 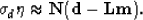 |
(5) |
Noise covariance for velocity estimation
Using the multiple realization methodology for velocity estimation problem
posed in the manner results in several difficulties.
First, what I would ideally like is a model of the noise.
This poses the problem of how to get the noise inverse covariance.
The first obstacle is that our data is generally a uniform
function of angle 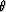 and a non-uniform function of
and a non-uniform function of  .What we would really like is a uniform function of just space.
We can get this by first removing the angle portion of
our data.
.What we would really like is a uniform function of just space.
We can get this by first removing the angle portion of
our data.
I obtain 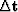 by finding the moveout parameter
by finding the moveout parameter 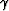 that best describes the moveout in migrated angle gathers.
I calculate
that best describes the moveout in migrated angle gathers.
I calculate 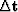 by mapping my selected
by mapping my selected 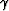 parameter
back into residual moveout and the multiplying by the local
velocity. Conversely I can write my
fitting goals in terms of
parameter
back into residual moveout and the multiplying by the local
velocity. Conversely I can write my
fitting goals in terms of 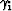 by
introducing an operator
by
introducing an operator 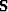 that maps
that maps 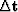 to
to 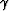 ,
,
| 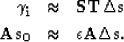 |
(6) |
| |
Making the data a uniform function of space is even easier.
I can easily write an operator that maps my irregular 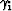 to
a regular function of
to
a regular function of 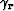 by a simple inverse
interpolation operator
by a simple inverse
interpolation operator 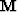 .I then obtain a new set of fitting goals,
.I then obtain a new set of fitting goals,
| 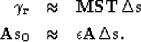 |
(7) |
| |
On this regular field the noise inverse covariance 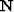 is easier
to get a handle on. We can approximate the noise inverse covariance
as a chain of two operators. The first,
is easier
to get a handle on. We can approximate the noise inverse covariance
as a chain of two operators. The first, 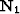 , f a fairly traditional
diagonal operator that amounts for uncertainty in our measurements.
For the tomography problem this translate into the width of
our semblance blob. For the second operator we
can estimate a Prediction Error Filter (PEF) on
, f a fairly traditional
diagonal operator that amounts for uncertainty in our measurements.
For the tomography problem this translate into the width of
our semblance blob. For the second operator we
can estimate a Prediction Error Filter (PEF) on 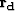 Guitton (2000) after solving
Guitton (2000) after solving
| 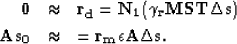 |
(8) |
| |
If we combine all these points and add in the data variance we get,
| 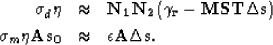 |
(9) |
| |





Next: About this document ...
Up: Clapp: Effect of velocity
Previous: AVA analysis
Stanford Exploration Project
6/8/2002
![]() :
:
![]() and a non-uniform function of
and a non-uniform function of ![]() .What we would really like is a uniform function of just space.
We can get this by first removing the angle portion of
our data.
.What we would really like is a uniform function of just space.
We can get this by first removing the angle portion of
our data.
![]() by finding the moveout parameter
by finding the moveout parameter ![]() that best describes the moveout in migrated angle gathers.
I calculate
that best describes the moveout in migrated angle gathers.
I calculate ![]() by mapping my selected
by mapping my selected ![]() parameter
back into residual moveout and the multiplying by the local
velocity. Conversely I can write my
fitting goals in terms of
parameter
back into residual moveout and the multiplying by the local
velocity. Conversely I can write my
fitting goals in terms of ![]() by
introducing an operator
by
introducing an operator ![]() that maps
that maps ![]() to
to ![]() ,
,
![]() to
a regular function of
to
a regular function of ![]() by a simple inverse
interpolation operator
by a simple inverse
interpolation operator ![]() .I then obtain a new set of fitting goals,
.I then obtain a new set of fitting goals,
