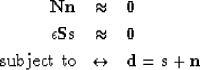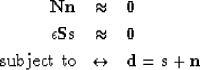Next: Preconditioning the filtering method
Up: From the filtering to
Previous: Definitions
Abma (1995) solved a
constrained least-squares problem to separate signal from
spatially uncorrelated noise:
| 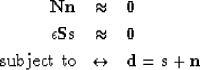 |
|
| (2) |
| |
The first equation defines mathematically the annihilation filter
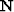 whereas the second equation defines the annihilation filter
whereas the second equation defines the annihilation filter
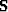 .
Minimizing in a least-squares sense the
fitting goals in equation (2) with respect
to
.
Minimizing in a least-squares sense the
fitting goals in equation (2) with respect
to  leads to the following expression for the estimated signal:
leads to the following expression for the estimated signal:
| 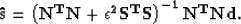 |
(3) |
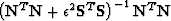 is a projection filter. I call it
the filtering method because the noise components are filtered out
by the PEF
is a projection filter. I call it
the filtering method because the noise components are filtered out
by the PEF 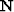 in equation (3).
in equation (3).





Next: Preconditioning the filtering method
Up: From the filtering to
Previous: Definitions
Stanford Exploration Project
6/7/2002