Least-squares inversion of a velocity stack

To make the velocity stack usable for other processing steps such as multiple removal, I should try to incorporate the PEF described above into an inversion scheme that compensates for energy removed during the filtering.

Following the ``trial solution'' approach described in Claerbout (1999), I change the variables $\bf {m=Pp}$ and solve equation (1) for the preconditioned variable $\bf{p}$:

$$\begin{eqnarray} \bf HPp - d &\approx& \bf 0\end{eqnarray}$$ (2)

Operator $\bf{P}$ in equation (2) is a cascade of two filters described in the previous section. After finding a solution for $\bf{p}$,I evaluate $\bf {m=Pp}$ to obtain the solution of the original problem. To avoid high frequency noise in the model, I introduce a regularization term into the problem and solve the system of equations:

$$\begin{eqnarray} \bf HPp - d &\approx& \bf 0 \nonumber \\ \bf \epsilon Ap &\approx& \bf 0\end{eqnarray}$$ (3)

In this paper I used the laplacian as the regularization operator $\bf{A}$ in equation (3).

Figure 5 shows the solution to the least-squares problem [equation (1)] after 25 iterations of the conjugate-gradient method, the velocity stack after the filtering, and the solution to the preconditioned least-squares problem [equation (3)] after 25 iterations of the conjugate-gradient.

 

prec
Figure 5 Left: Velocity stack after 25 iterations without preconditioning. Center: Velocity stack after filtering. Right: Velocity stack after 25 iterations with preconditioning.

Figure 6 shows the residual for the preconditioned problem [equation (3)] and the problem without preconditioning [equation (1)].

 

res_ann Figure 6 CG convergence with and without preconditioning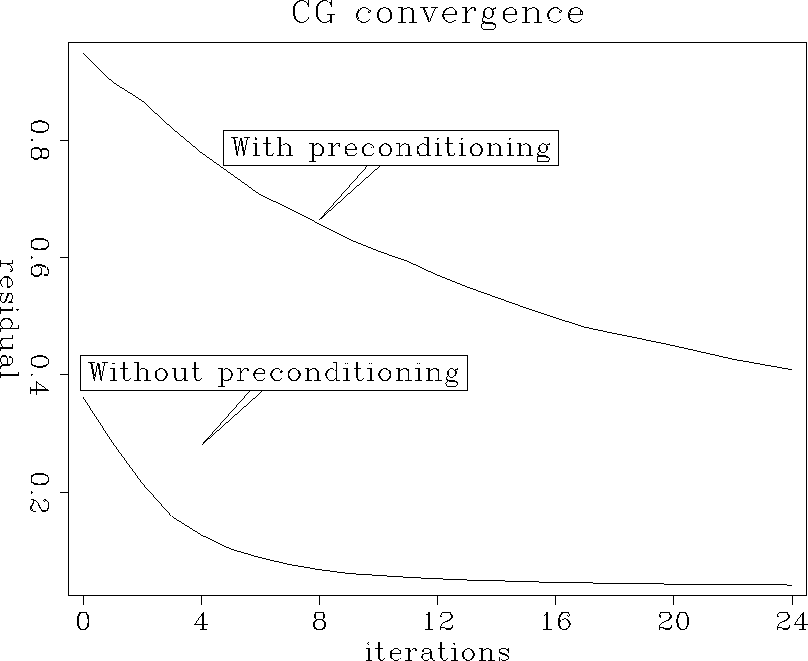

As Figures 5 and 6 show, although the solution for the preconditioned problem does not have artifacts, it converges much slower than the solution to the problem without preconditioning, which probably makes this method of preconditioning impractical.