Filter Design

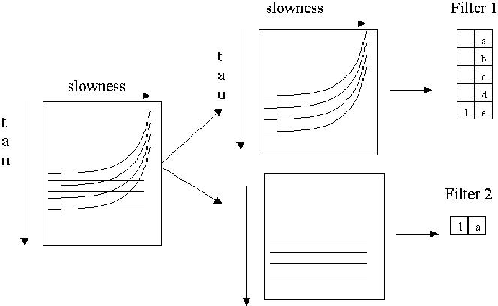
To design an operator to remove artifacts from a velocity stack, I am going to use the property of a two-column PEF to destroy a plane wave Claerbout (1999). Since artifacts from the far offset have a variable dip; this filter will need to be non-stationary. To design the operator we need to model the artifacts. The model of the artifacts can be created by applying the operator 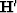${\bf H'}$ to the first and the last trace of the data (Figure 2). We should be able to describe such a model with a three-column-wide filter. However, it is easier to divide the model of the artifacts into a ``horizontal'' and a ``vertical'' parts. We then create a pair of two-column PEF and train one on the ``horizontal'' and the other on the ``vertical'' part of the noise model. These two filters may then be applied to a velocity stack one after another to destroy the artifacts. It is very important to notice that it is not necessary to use traces from real data to model the ``noise.'' Figure 2 illustrates how these separated parts of the ``noise'' model will look.

 

noise
Figure 2 Illustration of different parts of a noise model

Using this approach, we could create the noise model and PEF only once and then re-use them when needed. This would greatly reduce the cost of the procedure and allow for the design of a stable filter. Designing a stable non-stationary PEF is the most difficult task in any application that uses a non-stationary PEF. However, in this case I have the advantage of being able to compute a non-stationaty PEF before the processing, so I can use various methods of smoothing the filter coefficients. I can also change the ``noise'' model, which might be important if I try to use this filter in any least-squares inversion schemes later.