




Next: Space variable damping in
Up: Valenciano et al.: Multidimensional
Previous: Multidimensional deconvolution imaging condition
Changing deconvolution for convolution, a different imaging condition can be stated for each time in terms of the following fitting goal:
| 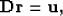 |
(4) |
where 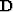 is a convolution matrix in which columns are downshifted versions of the downgoing wavefield
is a convolution matrix in which columns are downshifted versions of the downgoing wavefield 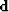 .
.
The least squares solution to this problem is
A damped solution is usually used to guarantee 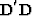 to be invertible as in
where
to be invertible as in
where  is a small positive number to guarantee no zeroes in
is a small positive number to guarantee no zeroes in 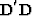 diagonal.
This is equivalent to the fitting goal
diagonal.
This is equivalent to the fitting goal
| 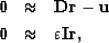 |
(5) |
| |
where 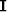 is the identity matrix that is used here as the regularization operator. Using this regularization scheme we are adding to the denominator a constant value where it is needed and where it is not.
is the identity matrix that is used here as the regularization operator. Using this regularization scheme we are adding to the denominator a constant value where it is needed and where it is not.
As it is our intention to use the previous knowledge of how the image should be, we could choose an smarter way to fill the zero values off 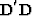 diagonal. We can substitute the regularization operator for one constructed with a priori information, using
diagonal. We can substitute the regularization operator for one constructed with a priori information, using
| 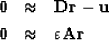 |
(6) |
| |
where our regularization operator 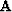 could be a steering filter Clapp et al. (1997). Steering filters can efficiently guide the solution toward a more geologically appealing form. This type of filter has been used with success to smooth existing reflectors and fill shadow zones in least squares inversion Prucha and Biondi (2002).
could be a steering filter Clapp et al. (1997). Steering filters can efficiently guide the solution toward a more geologically appealing form. This type of filter has been used with success to smooth existing reflectors and fill shadow zones in least squares inversion Prucha and Biondi (2002).





Next: Space variable damping in
Up: Valenciano et al.: Multidimensional
Previous: Multidimensional deconvolution imaging condition
Stanford Exploration Project
6/10/2002
![]() diagonal. We can substitute the regularization operator for one constructed with a priori information, using
diagonal. We can substitute the regularization operator for one constructed with a priori information, using