Multidimensional deconvolution imaging condition

Claerbout (1971) expresses the reflector mapping principle by the formula  

$${\bf r}(x,z)=\frac{ {\bf u}(x,z,t_{d})}{ {\bf d}(x,z,t_{d})},$$ (1)

where x is the horizontal coordinate, z is the depth, t_d is the time at which the downgoing wave ${\bf d}(x,z,t_{d})$ and the upgoing wave ${\bf u}(x,z,t_{d})$ coincide in time. This principle states that for time equal t_d the reflectivity strength ${\bf r}(x,z)$ depends only on the downgoing wave at (x,z) and on the upgoing wave at (x,z). No particular distribution is assumed for the reflectivity in the horizontal direction or in depth. Neither a dependence of the reflectivity of the future (wavefields anteceding t_d) or of the past (wavefields preceding t_d) is assumed.

Based on the imaging principle described in equation (1) we can propose a more general imaging condition that makes the reflectivity in (x,z) dependent on the downgoing and upgoing wavefields in the neighborhood of (x,y), shown in Figure 2 .

This more general imaging condition can be stated by:  

$${\bf r}(x,z)=\sum_{t}\frac{ {\bf u}([x-\sigma_x , x+\sigma_x... ...\bf d}([x-\sigma_x , x+\sigma_x ],[z-\sigma_z , z+\sigma_z ])},$$ (2)

where the division symbol ($\frac{\hspace{0.07in} }{\hspace{0.07in} }$) means 2-D deconvolution of the upgoing wavefield with the downgoing wavefield in the (x,z) plane. The $\sigma_x, \sigma_z$ are small numbers that define a rectangular neighborhood (x,y). This 2-D imaging condition states that there will be more than one point in the downgoing wavefield $\bf d$ and the upgoing wavefield $\bf u$ contributing to the strength at the point (x,y).

 

cuboxfig Figure 2 Multidimensional imaging geometry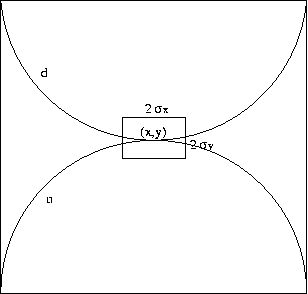

To address the multidimensional deconvolution we can make use of the helix concept Claerbout (1998). If we put the upgoing and the downgoing wavefields in helical coordinates, we will be able to treat the multidimensional deconvolution as a 1-D deconvolution.

But deconvolution is not an easy task. To have a stable deconvolution we need $\bf d$ to be minimum phase, so an approximation of equation (2) could be  

$$\bf r=\sum_{t}\frac{ u}{ d_{mp}},$$ (3)

where $\bf d_{mp}$ can be computed in an helix by means of Wilson spectral factorization Sava et al. (1998) in spatial coordinates (x,y) or by means of Kolmogoroff spectral factorization Claerbout (1976) in the Fourier domain.

Now, a new question arises: Does the new imaging condition formulation equation (3) honor Claerbout (1971) imaging principle?

The answer to this question is no, equation (3) gives a shifted version of the image. The minimum phase transformation produces a shift in spatial coordinates (x,y). This shift has to be calculated to obtain a properly placed image.

Some attempts were made to implement the anteceding procedure using Wilson spectral factorization to obtain a minimum phase version of the downgoing wavefield. No convergence of factorization results were obtained. More work needs to be done to understand the causes.