Introduction

For simple velocity models (e.g. constant v) a one-to-one mapping exists between recording offset ($\vert\vec{s}-\vec{g}\vert$) on the surface and incidence angle. Early amplitude versus offset (AVO) studies took advantage of this fact: authors looked at amplitude variation of events in common-midpoint gathers after normal moveout (NMO). It soon became clear, however, that NMO does not adequately correct for the focusing aspects of wave propagation, and that amplitude studies should be conducted after migration Resnick et al. (1987).

Kirchhoff migration algorithms can easily migrate data recorded at different offsets separately, and produce common-image point (CIP) gathers with migrated amplitude versus offset. Alternatively, interpreters often compare amplitude on near-offset migration images with far-offset images to look for anomalies linked to the presence of hydrocarbons. However, offset on the surface is a data-space parameter, whereas incidence angle is a model-space parameter; even for many relatively simple v(z) velocity models, no simple relationship exists between surface offset and incidence angle at the reflector.

For Kirchhoff amplitude versus angle (AVA) studies, all offsets need to be migrated, and the incidence angle determined at the imaging step by ray-tracing. Two disadvantages of this process are that it is sensitive to the stability of the ray-paths, and complicates the algorithm's I/O requirements.

de Bruin et al. (1990) first described how to calculate angle-dependent reflectivity with a wave-equation migration process. Their algorithm is appropriate for shot-profile algorithms, and involves a local slant-stack as part of the image-forming step. Similarly, Prucha et al. (1999) describe how to extract angle domain common-image-point gathers during shot-geophone migration in the offset-midpoint domain. Since these two migration methods are based on finite-frequency solutions to the wave-equation, there is no sensitivity to ray-traced angles. There is also no significantly increased I/O burden over zero-offset imaging with the same algorithm other than the need to output another model-space axis.

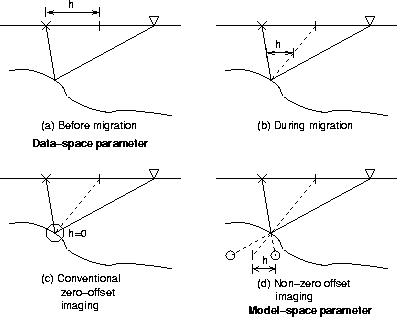
After wave equation migration, offset no longer refers to the recording offset at the surface, but rather refers to the subsurface offset between upgoing and downgoing wavefields. Offset after migration is therefore a model-space rather than a data-space parameter. Figure  graphically illustrates the meaning of offset before, during, and after migration.

 

offsetexp
Figure 1 Illustration of offset before (a), during (b), and after (c,d) migration.

For shot-geophone migration in the offset-midpoint domain, Sava and Fomel (2000) provide an algorithm that converts CIGs in the offset domain to angle gathers. The authors offer this as an alternative to Prucha et al.'s approach which requires extracting offset ray-parameter gathers as part of the migration imaging condition.