




Next: Shot to midpoint transformations
Up: Common-image gathers for shot-profile
Previous: Introduction
I produce angle gathers for shot-profile migrations by combining
de Bruin et al.'s 1990 approach with that of
Sava and Fomel (2000).
Rather than extracting a single zero-offset/zero-time reflectivity
image, I extract multiple zero-time images with a range of offsets.
In 2-D this can be performed with the following sum over frequency:
| 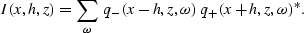 |
(128) |
Gathers produced this way contain off-diagonal elements of Berkhout's
reflectivity matrix 1985, and are equivalent to those
produced by imaging multiple non-zero offsets in an offset-midpoint
shot-geophone migration.
Consequently, the offset axes can be mapped to angle with Sava
and Fomel's 2000 transformation, which is
based on the relationship
| 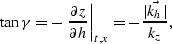 |
(129) |
where 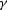 is the half-opening angle.
The imaging condition (t=0) provides the constant t, and the
common midpoint nature of CIGs provides the constant x, allowing
is the half-opening angle.
The imaging condition (t=0) provides the constant t, and the
common midpoint nature of CIGs provides the constant x, allowing
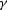 to be obtained directly from CIGs.
to be obtained directly from CIGs.





Next: Shot to midpoint transformations
Up: Common-image gathers for shot-profile
Previous: Introduction
Stanford Exploration Project
5/27/2001